
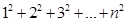 .但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道
.但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道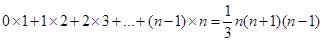 时,我们可以这样做:
时,我们可以这样做: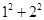 =(1+0)×1+(1+1)×2=l+0×1+2+1×2=(1+2)+(0×1+1×2)
=(1+0)×1+(1+1)×2=l+0×1+2+1×2=(1+2)+(0×1+1×2) =(1+0)×1+(1+1)×2+(l+2)×3
=(1+0)×1+(1+1)×2+(l+2)×3 =(1+0)×1+(1+1)×2+(l+2)×3+(1+3)×4;
=(1+0)×1+(1+1)×2+(l+2)×3+(1+3)×4;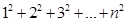 =(1+0)×1+(1+1)×2+(1+2)×3+…[(1+(n-l)]n
=(1+0)×1+(1+1)×2+(1+2)×3+…[(1+(n-l)]n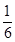 ×(___________)
×(___________)科目:初中数学 来源:不详 题型:填空题
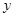 (千米)与时间
(千米)与时间 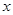 (小时)之间的函数关系如图3所示 当时 0≤x≤1,
(小时)之间的函数关系如图3所示 当时 0≤x≤1,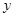 关于
关于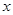 的函数解析式为
的函数解析式为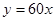 ,那么当 1≤
,那么当 1≤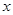 ≤2时,y关于x的函数解析式为______________ .
≤2时,y关于x的函数解析式为______________ . 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
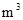 时,按2元/
时,按2元/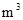 计费;月用水量超过20
计费;月用水量超过20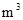 时,其中的20
时,其中的20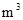 仍按2元/
仍按2元/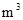 收费,超过部分按
收费,超过部分按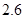 元/
元/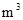 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为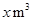 时,应交水费
时,应交水费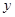 元.
元.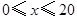 和
和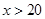 时
时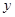 与
与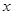 的函数表达式;
的函数表达式;| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 42.6元 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
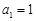 ,
,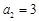 ,
,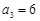 ,
,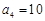 ,…;
,…;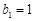 ,
,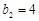 ,
,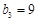 ,
,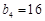 ,…;
,…;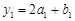 ,
,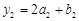 ,
,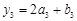 ,
,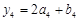 ,…,那么,按此规定,
,…,那么,按此规定,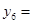 ,
,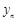 = (用含n的式子表示,n为正整数).
= (用含n的式子表示,n为正整数).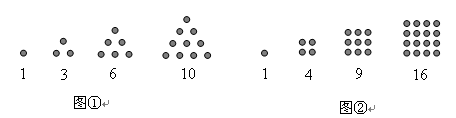
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
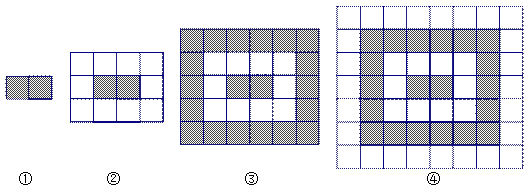
| 图形序号数 | ① | ② | ③ | ④ | … |
| 地砖总数(包括黑白地砖) | 2 | | | | |
 个图形一共用去地砖多少块?(用含
个图形一共用去地砖多少块?(用含 的代数式表示)
的代数式表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com