
【题目】如图1在平面直角坐标系中.等腰Rt△OAB的斜边OA在x轴上.P为线段OB上﹣动点(不与O,B重合).过P点向x轴作垂线.垂足为C.以PC为边在PC的右侧作正方形PCDM.OP= ![]() t、OA=3.设过O,M两点的抛物线为y=ax2+bx.其顶点N(m,n)
t、OA=3.设过O,M两点的抛物线为y=ax2+bx.其顶点N(m,n)
(1)写出t的取值范围 , 写出M的坐标:();
(2)用含a,t的代数式表示b;
(3)当抛物线开向下,且点M恰好运动到AB边上时(如图2)
①求t的值;
②若N在△OAB的内部及边上,试求a及m的取值范围.
【答案】
(1)解:0<t< ![]() ;2t,t
;2t,t
(2)
解:把M(2t,t)代入到y=ax2+bx中得:
t=4at2+2tb,
1=4at+2b,
b= ![]() ;
;
(3)
解:①如图2,∵OB= ![]() ,OP=
,OP= ![]() t,
t,
∴PB= ![]() ﹣
﹣ ![]() t,
t,
∵PM∥OA,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t=1;
②由(2)得:b= ![]() =
= ![]() ﹣2a,即4a=1﹣2b,
﹣2a,即4a=1﹣2b,
顶点N(﹣ ![]() ,﹣
,﹣ ![]() )(a<0,b>0),
)(a<0,b>0),
i)当0≤﹣ ![]() ≤
≤ ![]() 时,即a≤﹣
时,即a≤﹣ ![]() 时,
时,
﹣ ![]() ≥﹣
≥﹣ ![]() ,解得a≥﹣
,解得a≥﹣ ![]() ,
,
∴﹣ ![]() ≤a≤﹣
≤a≤﹣ ![]() ,
,
ii)当 ![]() <﹣
<﹣ ![]() ≤3时,即﹣
≤3时,即﹣ ![]() <a≤﹣
<a≤﹣ ![]() ,
,
3﹣(﹣ ![]() )≥﹣
)≥﹣ ![]() ,
,
b2﹣4b+3≤0,
1≤b≤3,
1≤ ![]() ﹣2a≤3,﹣
﹣2a≤3,﹣ ![]() ≤a≤﹣
≤a≤﹣ ![]() ,
,
则﹣ ![]() <a≤﹣
<a≤﹣ ![]() ,
,
综上所述:a的取值为:﹣ ![]() ≤a≤﹣
≤a≤﹣ ![]() ,
,
m=﹣ ![]() =1﹣
=1﹣ ![]() ,
,
得:4am=4a﹣1,a=﹣ ![]() =
= ![]() ,
,
﹣ ![]() ≤
≤ ![]() ≤﹣
≤﹣ ![]() ,
,
∴ ![]() ≤m≤2.
≤m≤2.
【解析】 解:(1)如图1,∵△OAB为等腰直角三角形,OA=3,
∴OB=AB= ![]() =
= ![]() ,
,
∵P为线段OB上﹣动点(不与O,B重合),
∴0< ![]() t<
t< ![]() ,
,
∴0<t< ![]() ,
,
∵四边形PCDM为正方形,
∴∠PCO=90°,
∵∠POC=45°,
∴△POC为等腰直角三角形,
∵OP= ![]() t,
t,
∴PC=OC=t,
∴OD=t+t=2t,
∴M(2t,t);
【考点精析】掌握二次函数的图象是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,其斜坡CD坡比为1: ![]() ,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
(1)求点E距水平面BC的高度;
(2)求楼房AB的高.(结果精确到0.1米,参考数据 ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论,其中正确结论是( )
A.b2<4ac
B.2a+b=0
C.a+b+c>0
D.若点B( ![]() ,y1)、C(
,y1)、C( ![]() ,y2)为函数图象上的两点,则y1<y2
,y2)为函数图象上的两点,则y1<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,若点A(﹣1,y1)、B(﹣6,y2)是它图象上的两点,则y1与y2的大小关系是( )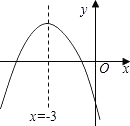
A.y1<y2
B.y1=y2
C.y1>y2
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有几个?
(1)AE平分∠DAB;(2)△EBA≌△DCE; (3)AB+CD=AD;(4)AE⊥DE;(5)AB//CD;
大家一起热烈地讨论交流,小红第一个得出正确答案,是( ).

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图所示 AD、AE分别是△ABC的中线、高,且AB=5cm,AC=3cm,,则△ABD与△ACD的周长之差为_________,△ABD与△ACD的面积关系为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
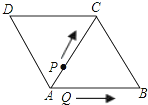
【题目】如图,△ABC和△ACD都是边长为2厘米的等边三角形,两个动点P,Q同时从A点出发,点P以0.5厘米/秒的速度沿A→C→B的方向运动,点Q以1厘米/秒的速度沿A→B→C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动。设P、Q运动的时间为t秒
(1)当t=2时,PQ=___;
(2)求点P、Q从出发到相遇所用的时间;
(3)当t取何值时,△APQ是等边三角形;请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: 
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com