
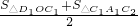 ,S右2=
,S右2=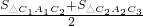 ).
). ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.
 ×2×|x+2|=21,
×2×|x+2|=21, ×2(2n-1+2)=2n+1,
×2(2n-1+2)=2n+1, ×2(2n-2+2+2n+2)=4n+2.
×2(2n-2+2+2n+2)=4n+2. (3)∵以OA1=2为底边做等腰三角形,∴A1的坐标为:(2,0),
(3)∵以OA1=2为底边做等腰三角形,∴A1的坐标为:(2,0), ,解得:
,解得: ,
, x2-
x2- x-2,
x-2, ×2×3=6.
×2×3=6. .
. ×4×[x+2-(
×4×[x+2-( x2-
x2- x-2)]=
x-2)]= ×6,
×6, x2-
x2- x-2=-2.
x-2=-2. x2-
x2- x-2=0.
x-2=0. (x+1)[
(x+1)[ +y-5]=
+y-5]= ×6,
×6, x2-
x2- x-8=0,
x-8=0, .
. 时,y=
时,y= x2-
x2- x-2=7+
x-2=7+ .
. 时,y=
时,y= x2-
x2- x-2=7-
x-2=7- .
. ,7+
,7+ ),P4(1-
),P4(1- ,7-
,7- ).
). ,7+
,7+ ),P4(1-
),P4(1- ,7-
,7- ).
). ,然后分两种情况进行讨论:①点P在直线y=x+2的下方,②点P在直线y=x+2的上方.针对这两种情况,都可以根据△PD1C2的面积是△C1OD1与△C1A1C2面积和的
,然后分两种情况进行讨论:①点P在直线y=x+2的下方,②点P在直线y=x+2的上方.针对这两种情况,都可以根据△PD1C2的面积是△C1OD1与△C1A1C2面积和的 ,列出方程,解方程即可.
,列出方程,解方程即可.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A1B1C1D1E1,已知OA=10cm,OA1=20cm,五边形ABCDE的面积为50cm2,则五边形A1B1C1D1E1的面积为
如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A1B1C1D1E1,已知OA=10cm,OA1=20cm,五边形ABCDE的面积为50cm2,则五边形A1B1C1D1E1的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
| S△D1OC1+S△C1A1C2 |
| 2 |
| S△C1A1C2+S△C2A2C3 |
| 2 |
| 4 |
| 3 |

查看答案和解析>>
科目:初中数学 来源:2012年浙江省杭州市拱墅区下城区中考数学一模试卷(解析版) 题型:解答题
 ,S右2=
,S右2= ).
). ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012年江苏省无锡市江阴市初级中学中考数学模拟试卷(解析版) 题型:解答题
 ,S右2=
,S右2= ).
). ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com