
分析 (1)根据方程有两个不相等的实数根可得△=[-(2k-3)]2-4(k2+1)=4k2-12k+9-4k2-4=-12k+5>0,求出k的取值范围;
(2)首先判断出两根均小于0,然后去掉绝对值,进而得到-2k+3=2k2+2-3,结合k的取值范围解方程即可.
解答 解:(1)∵原方程有两个不相等的实数根,
∴△=[-(2k-3)]2-4(k2+1)=4k2-12k+9-4k2-4=-12k+5>0,
解得:k<$\frac{5}{12}$;
(2)∵k<$\frac{5}{12}$,
∴x1+x2=2k-3<0,
又∵x1•x2=k2+1>0,
∴x1<0,x2<0,
∴|x1|+|x2|=-x1-x2=-(x1+x2)=-2k+3,
∵|x1|+|x2|=2|x1x2|-3,
∴-2k+3=2k2+2-3,即k2+k-2=0,
∴k1=1,k2=-2,
又∵k<$\frac{5}{12}$,
∴k=-2.
点评 此题考查了一元二次方程ax2+bx+c=0根的判别式和根与系数的关系的应用,(1)△>0时,方程有两个不相等的实数根;(2)△=0时,方程有两个相等的实数根;(3)△<0时,方程没有实数根;(4)x1+x2=-$\frac{b}{a}$;(5)x1•x2=$\frac{c}{a}$.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:选择题
| A. | 了解我国东海水域是否受到日本核辐射污染 | |
| B. | 了解我们班50名同学上次月考数学成绩 | |
| C. | 了解一批节能灯泡的使用寿命 | |
| D. | 了解一批我国最新生产的核弹头的杀伤半径 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
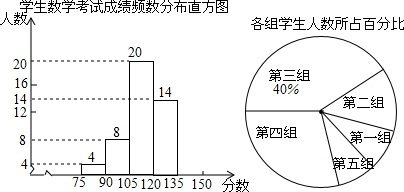
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
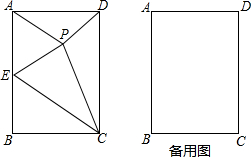 如图,在矩形ABCD中,AB=16,AD=12,E是AB上一点,连接CE,现将∠B向右上方翻折,折痕为CE,使点B落在点P处.
如图,在矩形ABCD中,AB=16,AD=12,E是AB上一点,连接CE,现将∠B向右上方翻折,折痕为CE,使点B落在点P处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).
如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课时间的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分),请问:
心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课时间的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分),请问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com