
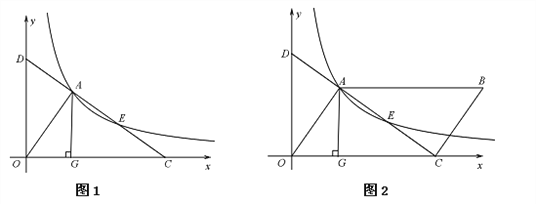
【题目】如图1,直线![]() 交x轴于点C,交y轴于点D,与反比例函数
交x轴于点C,交y轴于点D,与反比例函数![]() 的图像交于两点A、E,AG⊥x轴,垂足为点G,S△AOG=3.
的图像交于两点A、E,AG⊥x轴,垂足为点G,S△AOG=3.
(1)k = ;
(2)求证:AD =CE;
(3)如图2,若点E为平行四边形OABC的对角线AC的中点,求平行四边形OABC的面积
【答案】(1)k=6;
(2)证明见解析;
(3)S平行四边形OABC=18
【解析】(1)设A(m,n),由题意 ![]() OGAG=3,推出mn=6,由点A在y=
OGAG=3,推出mn=6,由点A在y=![]() 上,推出k=mn=6.
上,推出k=mn=6.
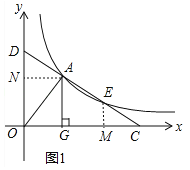
(2)如图1中,作AN⊥OD于N,EM⊥OC于M.设直线CD的解析式为y=k′x+b,A(x1,y1),E(x2,y2).首先证明EM=﹣k′AN,EM=﹣k′MC,推出AN=CM,再证明△DAN≌△ECM,即可解决问题.
(3)如图2中,连接GD,GE.由EA=EC,AD=EC,推出AD=AE=EC,推出S△ADG=S△AGE=S△GEC=3,求出△AOC的面积即可解决问题.
试题解析:
(1)解:设A(m,n),
∵![]() OGAG=3,
OGAG=3,
∴![]() mn=3,
mn=3,
∴mn=6,
∵点A在y=![]() 上,
上,
∴k=mn=6.
(2)证明:如图1中,作AN⊥OD于N,EM⊥OC于M.设直线CD的解析式为y=k′x+b,A(x1,y1),E(x2,y2).
则有y1=k′x1+b,y2=k′x2+b,
∴y2﹣y1=k′(x2﹣x1),
∴![]() ﹣
﹣![]() =k′(x2﹣x1),
=k′(x2﹣x1),
∴﹣k′x1x2=6,
∴﹣k′x1=![]() ,
,
∴y2=﹣k′x1,
∴EM=﹣k′AN,
∵D(0,b),C(﹣![]() ,0),
,0),
∴tan∠DCO=![]() =﹣k′=
=﹣k′=![]() ,
,
∴EM=﹣k′MC,
∴AN=CM,
∵AN∥CM,
∴∠DAN=∠ECM,
在△DAN和△ECM中,
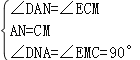 ,
,
∴△DAN≌△ECM,
∴AD=EC.
(3)解:如图2中,连接GD,GE.
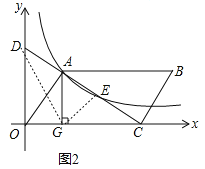
∵EA=EC,AD=EC,
∴AD=AE=EC,
∴S△ADG=S△AGE=S△GEC=3,
∵S△AOG=S△ADG=3,
∴S△AOC=3+3+3=9,
∴平行四边形ABCD的面积=2S△AOC=18.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的情境对话,然后解答问题

(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt![]() ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt![]() ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
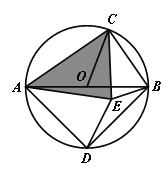
求证:![]() ACE是奇异三角形;
ACE是奇异三角形;
当![]() ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有A、B两个餐厅,甲、乙两名学生各自随机选择其中一个餐厅用餐,请用列表或画树状图的方法解答:
(1)甲、乙两名学生在同一餐厅用餐的概率;
(2)甲、乙两名学生至少有一人在B餐厅的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B对应的数分别为1、3,点P为数轴上一动点,其对应的数为x.![]()
(1)若点P到点A、点B的距离相等,点P对应的数是;
(2)数轴上,点P到点A、点B的距离之和为5,则x的值为;
(3)当点P以每秒1个单位长度的速度从原点O向左运动,同时点B以每秒3个单位长度的速度沿数轴向左运动(点A保持不动),当点P到点A、点B的距离相等时,求运动时间t的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①~④分别表示甲、乙两辆汽车在同一条路上匀速行驶中速度与时间的关系,小明对4个图中汽车运动的情况进行了描述,其中正确的是( )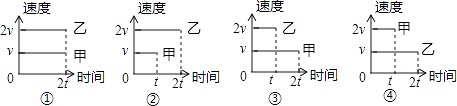
A.图①:乙的速度是甲的2倍,甲乙的路程相等
B.图②:乙的速度是甲的2倍,甲的路程是乙的一半
C.图③:乙的速度是甲的2倍,乙的路程是甲的一半
D.图④:甲的速度是乙的2倍,甲乙的路程相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com