
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпy=Љx+3гыxжсЁЂyжсЗжБ№НЛгкЕуBЁЂCЃЛХзЮяЯпy=Љx2+bx+cОЙ§BЁЂCСНЕуЃЌВЂгыxжсНЛгкСэвЛЕуAЃЎ
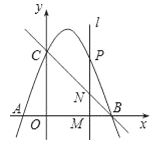
ЃЈ1ЃЉЧѓИУХзЮяЯпЫљЖдгІЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЩшPЃЈxЃЌyЃЉЪЧЃЈ1ЃЉЫљЕУХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїжБЯпlЁЭxжсгкЕуMЃЌНЛжБЯпBCгкЕуNЃЎ
ЂйШєЕуPдкЕквЛЯѓЯоФкЃЎЪдЮЪЃКЯпЖЮPNЕФГЄЖШЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧѓГіЫќЕФзюДѓжЕМАДЫЪБxЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЂкЧѓвдBCЮЊЕзБпЕФЕШбќЁїBPCЕФУцЛ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЫљЧѓКЏЪ§ЙиЯЕЪНЮЊy=Љx2+2x+3ЃЛ
ЃЈ2ЃЉЂйЯпЖЮPNЕФГЄЖШЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
Ђк![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉРћгУвЛДЮКЏЪ§гызјБъжсзјБъЧѓЗЈЃЌЕУГіBЁЂCСНЕуЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіЖўДЮКЏЪ§НтЮіЪНЃЎ
ЃЈ2ЃЉРћгУЖўДЮКЏЪ§зюжЕЧѓЗЈВЛФбЧѓГіЃЌдйРћгУШ§НЧаЮУцЛ§жЎМфЕФЙиЯЕЃЌПЩЧѓГіЕШбќЁїBPCЕФУцЛ§
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩгкжБЯпy=Љx+3ОЙ§BЁЂCСНЕуЃЌ
Сюy=0ЕУx=3ЃЛСюx=0ЃЌЕУy=3ЃЌ
ЁрBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉЃЌ
ЁпЕуBЁЂCдкХзЮяЯпy=Љx2+bx+cЩЯЃЌгкЪЧЕУ![]() ЃЌ
ЃЌ
НтЕУb=2ЃЌc=3ЃЌ
ЁрЫљЧѓКЏЪ§ЙиЯЕЪНЮЊy=Љx2+2x+3ЃЛ
ЃЈ2ЃЉЂйЁпЕуPЃЈxЃЌyЃЉдкХзЮяЯпy=Љx2+2x+3ЩЯЃЌ
ЧвPNЁЭxжсЃЌ
ЁрЩшЕуPЕФзјБъЮЊЃЈxЃЌЉx2+2x+3ЃЉЃЌ
ЭЌРэПЩЩшЕуNЕФзјБъЮЊЃЈxЃЌЉx+3ЃЉЃЌ
гжЕуPдкЕквЛЯѓЯоЃЌ
ЁрPN=PMЉNMЃЌ
=ЃЈЉx2+2x+3ЃЉЉЃЈЉx+3ЃЉЃЌ
=Љx2+3xЃЌ
=ЁЊ![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ
ЯпЖЮPNЕФГЄЖШЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
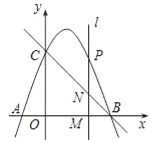
ЂкНтЃК
гЩЬтвтжЊЃЌЕуPдкЯпЖЮBCЕФДЙжБЦНЗжЯпЩЯЃЌ
гжгЩЂйжЊЃЌOB=OCЃЌ
ЁрBCЕФжаДЙЯпЭЌЪБвВЪЧЁЯBOCЕФЦНЗжЯпЃЌ
ЁрЩшЕуPЕФзјБъЮЊЃЈaЃЌaЃЉЃЌ
гжЕуPдкХзЮяЯпy=Љx2+2x+3ЩЯЃЌгкЪЧгаa=Љa2+2a+3ЃЌ
Ёрa2ЉaЉ3=0ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊЃК![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ШєЕуPЕФзјБъЮЊ![]() ЃЌДЫЪБЕуPдкЕквЛЯѓЯоЃЌ
ЃЌДЫЪБЕуPдкЕквЛЯѓЯоЃЌ
дкRtЁїOMPКЭRtЁїBOCжаЃЌMP=OM=![]() ЃЌ
ЃЌ
OB=OC=3ЃЌ
SЁїBPC=SЫФБпаЮBOCPЉSЁїBOC=2SЁїBOPЉSЁїBOCЃЌ
=![]() ЃЌ
ЃЌ
ШєЕуPЕФзјБъЮЊ![]() ЃЌДЫЪБЕуPдкЕкШ§ЯѓЯоЃЌ
ЃЌДЫЪБЕуPдкЕкШ§ЯѓЯоЃЌ
дђSЁїBPC=SЁїBOP+SЁїCOP+SЁїBOC=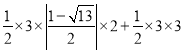 ЃЌ
ЃЌ
=![]() ЃЌ
ЃЌ
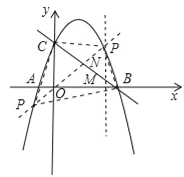


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
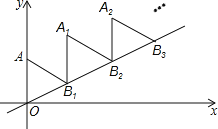
ЁОЬтФПЁПШчЭМЃЌЗХжУЕФЁїOAB1ЃЌЁїB1A1B2ЃЌЁїB2A2B3ЃЌЖМЪЧБпГЄЮЊ2ЕФЕШБпШ§НЧаЮЃЌБпAOдкYжсЩЯЃЌЕуB1ЁЂB2ЁЂB3ЖМдкжБЯпy=![]() xЩЯЃЌдђЕуA2019ЕФзјБъЮЊ__________________
xЩЯЃЌдђЕуA2019ЕФзјБъЮЊ__________________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() дк
дк![]() ЕФжБОЖ
ЕФжБОЖ![]() ЕФбгГЄЯпЩЯЃЌЕу
ЕФбгГЄЯпЩЯЃЌЕу![]() дк
дк![]() ЩЯЃЌЧвAC=CDЃЌЁЯACD=120Ёу.
ЩЯЃЌЧвAC=CDЃЌЁЯACD=120Ёу.
ЃЈ1ЃЉЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЕФАыОЖЮЊ2ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§.
ЕФАыОЖЮЊ2ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§.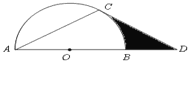
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдк 10ЁС6 ЕФе§ЗНаЮЭјИёжаЃЌУПИіаЁе§ЗНаЮЕФБпГЄОљЮЊ 1ЃЌЯпЖЮ AB ЕФЖЫЕу AЁЂB ОљдкаЁе§ЗНаЮЕФЖЅЕуЩЯЃЎ
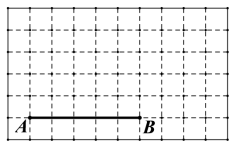
ЃЈ1ЃЉдкЭМжаЛГівд AB ЮЊвЛбќЕФЕШбќЁїABCЃЌЕу C дкаЁе§ЗНаЮЖЅЕуЩЯЃЌЁїABC ЮЊЖлНЧШ§НЧаЮЃЌЧвЁїABC ЕФУцЛ§ЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЭМжаЛГівд AB ЮЊаББпЕФжБНЧШ§НЧаЮ ABDЃЌ Еу DдкаЁе§ЗНаЮЕФЖЅЕуЩЯЃЌЧв AD>BDЃЛ
ЃЈ3ЃЉСЌНг CDЃЌЧыФужБНгаДГіЯпЖЮ CD ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЙцЖЈАбвЛИіЕуЯШШЦдЕуФцЪБеыа§зЊ45ЁуЃЌдйзїГіа§зЊКѓЕФЕуЙигкдЕуЕФЖдГЦЕуЃЌетГЦЮЊвЛДЮБфЛЛЃЌвбжЊЕуAЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЌдђЕуAОЙ§СЌај2018ДЮетбљЕФБфЛЛЕУЕНЕФЕуA2018ЕФзјБъЪЧ___ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпABгыХзЮяЯпCЃКyЃНax2+2x+cЯрНЛгкЕуA(Љ1ЃЌ0)КЭЕуB(2ЃЌ3)СНЕуЃЎ
(1)ЧѓХзЮяЯпCКЏЪ§БэДяЪНЃЛ
(2)ШєЕуMЪЧЮЛгкжБЯпABЩЯЗНХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЕБ![]() ЕФУцЛ§зюДѓЪБЃЌЧѓДЫЪБ
ЕФУцЛ§зюДѓЪБЃЌЧѓДЫЪБ![]() ЕФУцЛ§SМАЕуMЕФзјБъЃЎ
ЕФУцЛ§SМАЕуMЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуAЃЈ3ЃЌ3ЃЉЃЌЕуBЃЈ4ЃЌ0ЃЉЃЌЕуCЃЈ0ЃЌЉ1ЃЉЃЎ
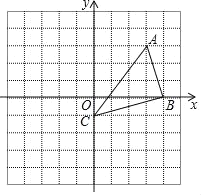
ЃЈ1ЃЉвдЕуCЮЊжааФЃЌАбЁїABCФцЪБеыа§зЊ90ЁуЃЌЧыдкЭМжаЛГіа§зЊКѓЕФЭМаЮЁїAЁфBЁфCЃЌЕуBЁфЕФзјБъЮЊ________ЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЧѓГіЕуAОЙ§ЕФТЗОЖ![]() ЕФГЄЃЈНсЙћБЃСєІаЃЉЃЎ
ЕФГЄЃЈНсЙћБЃСєІаЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
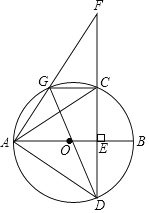
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвCDЁЭABгкЕуEЃЌGЪЧ![]() ЩЯвЛЖЏЕуЃЌAGЃЌDCЕФбгГЄЯпНЛгкЕуFЃЌСЌНгACЃЌADЃЌGCЃЌGDЃЎ
ЩЯвЛЖЏЕуЃЌAGЃЌDCЕФбгГЄЯпНЛгкЕуFЃЌСЌНгACЃЌADЃЌGCЃЌGDЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯFGCЃНЁЯAGDЃЛ
ЃЈ2ЃЉШєADЃН6ЃЎ
ЂйЕБACЁЭDGЃЌCGЃН2ЪБЃЌЧѓsinЁЯADGЃЛ
ЂкЕБЫФБпаЮADCGУцЛ§зюДѓЪБЃЌЧѓCFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=ax2+bx+cЕФЭМЯѓОЙ§ЕуЃЈ0ЃЌ1ЃЉЃЌЖдГЦжсЮЊжБЯпx=Љ1ЃЌЯТСаНсТлЃКЂйa+b+cЃМ0ЃЛЂкaЉb+cЃО1ЃЛЂлabcЃО0ЃЛЂм4aЉ2b+cЃО0ЃЛЂнcЉaЃО1ЃЎЦфжаЃЌе§ШЗНсТлЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
A. 2 B. 3 C. 4 D. 5
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com