
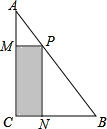
 如图,将直角三角形余料截出一个矩形PMCN,∠C=90°,AC=40cm,BC=30cm,点P、M、N分别在AB、AC、BC上,设CN=x.
如图,将直角三角形余料截出一个矩形PMCN,∠C=90°,AC=40cm,BC=30cm,点P、M、N分别在AB、AC、BC上,设CN=x.| PN |
| AC |
| BN |
| BC |
| PN |
| AC |
| BN |
| BC |
| PN |
| 40 |
| 30-x |
| 30 |
| 4(30-x) |
| 3 |
| 4(30-x) |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
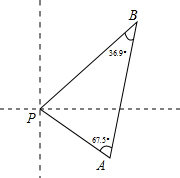 我南海巡逻船接到有人落水求救信号,如图,巡逻船A观测到∠PAB=67.5°,同时,巡逻船B观测到∠PBA=36.9°,两巡逻船相距63海里,求此时巡逻船A与落水人P的距离?(参考数据:sin36.9°≈
我南海巡逻船接到有人落水求救信号,如图,巡逻船A观测到∠PAB=67.5°,同时,巡逻船B观测到∠PBA=36.9°,两巡逻船相距63海里,求此时巡逻船A与落水人P的距离?(参考数据:sin36.9°≈| 3 |
| 5 |
| 3 |
| 4 |
| 12 |
| 13 |
| 12 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
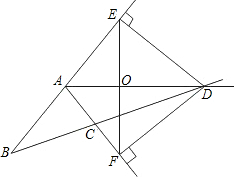 如图,在△ABC中,AB≠AC,∠BAC的外角平分线交直线BC于D,过D作DE⊥AB,DF⊥AC分别交直线AB,AC于E,F,连结EF.
如图,在△ABC中,AB≠AC,∠BAC的外角平分线交直线BC于D,过D作DE⊥AB,DF⊥AC分别交直线AB,AC于E,F,连结EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com