
【题目】函数y=x2﹣4x+3
(1)求其图象与x轴交点A、B的坐标(A在B左边);
(2)在坐标系中画出函数图象;
(3)若函数图形的顶点为C,求△ABC的面积.
【答案】(1)点A的坐标为(1,0),点B的坐标为(3,0);(2)详见解析;(3)1
【解析】
(1)根据题目中的函数解析式可以求得点A和点B的坐标;
(2)根据函数解析式可以求得该函数的顶点坐标,从而可以画出相应的函数图象;
(3)根据点A、B、C的坐标可以求得△ABC的面积.
解:(1)∵y=x2﹣4x+3=(x﹣1)(x﹣3),
∴当y=0时,x1=1,x2=3,
∴点A的坐标为(1,0),点B的坐标为(3,0);
(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴该抛物线的顶点坐标为(2,﹣1),
该函数的图象有右图所示;
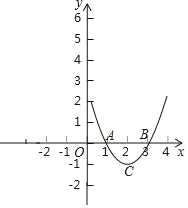
(3)由(2)知顶点C的坐标为(2,﹣1),
∵点A的坐标为(1,0),点B的坐标为(3,0),
∴AB=2,
∴△ABC的面积是:![]() AB×h=
AB×h=![]() =1.
=1.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
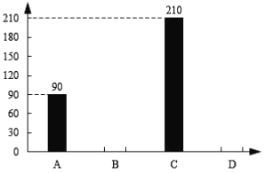
【题目】沙坪坝正在创建全国文明城市,其中垃圾分类是一项重要的举措.现随机抽查了沙区部分小区住户12月份某周内“垃圾分类”的实施情况,并绘制成了以下两幅不完整的统计图,图中![]() 表示实施天数小于5天,
表示实施天数小于5天,![]() 表示实施天数等于5天,
表示实施天数等于5天,![]() 表示实施天数等于6天,
表示实施天数等于6天,![]() 表示实施天数等于7天.
表示实施天数等于7天.
(1)求被抽查的总户数;
(2)补全条形统计图;
(3)求扇形统计图中![]() 的圆心角的度数.
的圆心角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
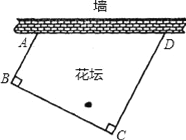
【题目】小区要用篱笆围成一个四边形花坛、花坛的一边利用足够长的墙,另三边所用的篱笆之和恰好为18米.围成的花坛是如图所示的四边形ABCD,其中∠ABC=∠BCD=90°,且BC=2AB.设AB边的长为x米.四边形ABCD面积为S平方米.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围).
(2)当x是多少时,四边形ABCD面积S最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们越来越注重营养健康,有一种有机水果![]() 在市场上特别受欢迎,某大型超市以10元/千克的价格在产地收购了6000千克
在市场上特别受欢迎,某大型超市以10元/千克的价格在产地收购了6000千克![]() 水果,立即将其冷藏,请根据下列信息解决问题:
水果,立即将其冷藏,请根据下列信息解决问题:
①水果![]() 的市场价每天每千克上涨0.1元;
的市场价每天每千克上涨0.1元;
②平均每天有10千克的该水果损坏,不能出售;
③每天的冷藏费用为300元;
④该水果最多保存110天;
(1)若将这批![]() 水果存放
水果存放![]() 天后一次性出售,则
天后一次性出售,则![]() 天后这批水果的销售单价为 元;
天后这批水果的销售单价为 元;
(2)将这批![]() 水果存放多少天后一次性出售所得利润为9600元?
水果存放多少天后一次性出售所得利润为9600元?
(3)将这批![]() 水果存放多少天后一次性出售可获得最大利润?最大利润是多少?
水果存放多少天后一次性出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB与抛物线C:y=ax2+2x+c相交于点A(﹣1,0)和点B(2,3)两点.
(1)求抛物线C函数表达式;
(2)若点M是位于直线AB上方抛物线上的一动点,当![]() 的面积最大时,求此时
的面积最大时,求此时![]() 的面积S及点M的坐标.
的面积S及点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD为菱形,点E、F、G、H分别为各边中点,判断E、F、G、H四点是否在同一个圆上,如果在同一圆上,找到圆心,并证明四点共圆;如果不在,说明理由.
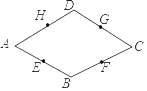
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的三条边为边,分别向外作正方形,连接EF,GH,DJ,如果△ABC的面积为8,则图中阴影部分的面积为( )

A.28B.24C.20D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是长为10m,倾斜角为30°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).(参考数据:sin65°=0.90,tan65°=2.14)
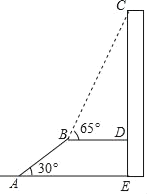
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com