
如图,在菱形ABCD中,AB=CD=10,∠BAD=60°,点M从点A以每秒1个单位长的速度沿着AD边向点D移动;设点M移动的时间为t秒(0≤t≤10),
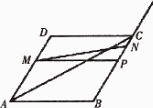
(1)点N为BC边上任意一点,在点M移动过程中的某一时刻,线段MN是否可以将菱形ABCD分割成面积相等的两部分?并说明理由;
(2)点N从点B(与点M出发的时刻相同)以每秒2个单位长的速度沿着BC边向点C移动,在什么时候梯形ABNM的面积最大?并求出面积的最大值;
(3)点N从点B(与点M出发的时刻相同)以每秒a(a≥2)个单位长的速度沿着射线BC方向(可以超越点C)移动,过点M作MP∥AB,交BC于点P,当△MPN≌△ABC时,设△MPN与菱形ABCD重叠部分的面积为S,求出用t表示S的关系式,并求当S=0时a的值.
|
解:(1)MN一定能在某一时刻将菱形ABCD分割成面积相等的两部分.…………(2分) 对于中心对称图形,过中心的任一直线均能将图形分割成面积相等的两部分. 而且菱形是中心对称图形,在点M由A到D的移动过程中,一定存在一个时刻,使得线段MN过菱形的中心. (2)过B作 在 最大面积为 (3) 当 过P作 设MN交DC于F, 当S=0,即 解得 |


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com