
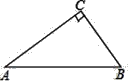
【题目】如图,在直角三角形ABC中,
(1)过点A作AB的垂线与∠B的平分线相交于点D
(要求:尺规作图,保留作图痕迹,不写作法);
(2)若∠A=30°,AB=2,则△ABD的面积为 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.
其中正确结论的序号是( )

A. ①②③④⑤ B. ①②③④ C. ①③④⑤ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分) | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n<90 | B | |
70≤n<80 | C | 15 |
n<70 | D | 6 |
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两地相距3200 m,小王、小李分别从甲、乙两地同时出发,相向而行,相遇后两人立即返回到各自出发地并停止行进.已知小李的速度始终是60 m/min,小王在相遇后以匀速返回,但比小李晚回到原地。在整个行进过程中,他们之间的距离y(m)与行进的时间t(min)之间的函数关系如图中的折线段AB—BC—CD所示,请结合图像信息解答下列问题:
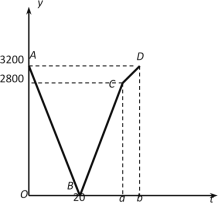
(1)小王返回时的速度= m/min,a= ,b= ;
(2)当t为何值时,小王、小李两人相距800 m?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△FPQ均是等边三角形,点D、E、F分别是△ABC三边的中点,点P在AB边上,连接EF、QE.若AB=6,PB=1,则QE= .
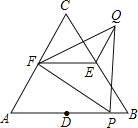
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过对下面数学模型的研究学习,解决下列问题:
(模型呈现)
(1)如图1,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .由
.由![]() ,得
,得![]() .又
.又![]() ,可以推理得到
,可以推理得到![]() .进而得到
.进而得到![]() _____,
_____,![]() _____.我们把这个数学模型称为“
_____.我们把这个数学模型称为“![]() 字”模型或“一线三等角”模型;
字”模型或“一线三等角”模型;
(模型应用)
(2)①如图2,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,且
,且![]() 于点
于点![]() ,
,![]() 与直线
与直线![]() 交于点
交于点![]() .求证:点
.求证:点![]() 是
是![]() 的中点.
的中点.
②如图3,在平面直角坐标系![]() 中,点
中,点![]() 为平面内任一点,点
为平面内任一点,点![]() 的坐标为
的坐标为![]() .若
.若![]() 是以
是以![]() 为斜边的等腰直角三角形,请直接写出点
为斜边的等腰直角三角形,请直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。
的图象过点(98,19),它与X轴的交点为(P,0),与y轴交点为(0,q),若p是质数,q是正整数,那么满足条件的所有一次函数的个数为( )。
A.0B.1C.2D.大于2的整数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一定能确定△ABC≌△DEF的条件是( )
A.AB=DE,BC=EF,∠A=∠DB.∠A=∠E,AB=EF,∠B=∠D
C.∠A=∠D,AB=DE,∠B=∠ED.∠A=∠D,∠B=∠E,∠C=∠F
查看答案和解析>>
科目:初中数学 来源: 题型:
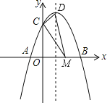
【题目】如图,对称轴为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() 点坐标为
点坐标为![]() 设抛物线的顶点为
设抛物线的顶点为![]() .
.
![]() 求抛物线的解析式及顶点坐标;
求抛物线的解析式及顶点坐标;
![]() 为
为![]() 轴上的一点,当
轴上的一点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标及
的坐标及![]() 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com