练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某批发商以40元/千克的成本价购入了某产品700千克，据市场预测，该产品的

    销售价y（元/千克）与保存时间x（天）的函数关系为y＝50+2x，但保存这批产品平均每天

    将损耗15千克，且最多保存15天．另外，批发商每天保存该批产品的费用为50元．

    （1）若批发商在保存该产品5天时一次性卖出，则可获利       元．

    （2）如果批发商希望通过这批产品卖出获利10000元，则批发商应在保存该产品多少

    天时一次性卖出？


    解：（1）9250    

    （2）设批发商应在保存该产品x天时一次性卖出，根据题意得：

    （700－15x）(50+2x)－50x－40×700＝10000，

    化简得：－30x2+600x－3000＝0，

    x2－20x+100＝0，（x－10）2＝0，

    解得：x 1＝x 2＝10，

    ∵10＜15，∴x＝10  

    答：批发商应在保存该产品10天时一次性卖出获利10000元．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    分式方程 ＝1- 的解为        ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


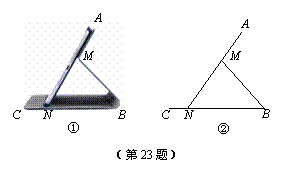
    图①为一种平板电脑保护套的支架效果图，AM固定于平板电脑背面，与可活动的MB、CB部分组成支架．平板电脑的下端N保持在保护套CB上．不考虑拐角处的弧度及平板电脑和保护套的厚度，绘制成图②．其中AN表示平板电脑，M为AN上的定点，AN＝CB＝20 cm，AM＝8 cm，MB＝MN．我们把∠ANB叫做倾斜角．

    （1）当倾斜角为45°时，求CN的长；

    （2）按设计要求，倾斜角能小于30°吗？请说明理由．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    用半径为6cm的半圆围成一个圆锥的侧面，则圆锥的底面半径等于          cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


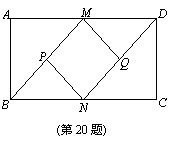
    如图，在矩形ABCD中，M、N分别AD、BC的中点，P、Q分别BM、DN

    的中点．

    （1）求证：四边形MPNQ是菱形；

    （2）若AB＝2，BC＝4，求四边形MPNQ的面积．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    利用表格中的数据，可求出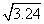＋(4.123)2－   的近似值是(结果保留整数)．

    a

    a2

    17

    289

    4.123

    13.038

    18

    324

    4.243

    13.416

    19

    361

    4.359

    13.784

    A．3

    B．4

    C．5

    D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     (2×103)2×(3×10－3) ＝                 ．（结果用科学计数法表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


         反比例函数y＝ (k为常数,k≠0)的图象是双曲线.当k＞0时，双曲线两个分支分别在

    一、三象限,在每一个象限内,y随x的增大而减小（简称增减性）；反比例函数的图象关于

       原点对称（简称对称性）．   

       这些我们熟悉的性质，可以通过说理得到吗？

      【尝试说理】

    我们首先对反比例函数y＝（k＞0）的增减性来进行说理．

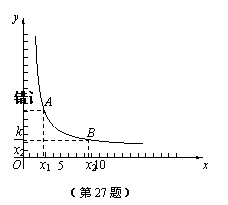
    如图，当x＞0时．

    在函数图象上任意取两点A、B，设A(x1，)，B(x2，)，

    且0＜x1＜ x2．

    下面只需要比较和的大小．

    —＝ ．

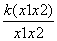    ∵0＜x1＜ x2，∴x1－x2＜0，x1 x2＞0，且 k＞0．

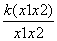    ∴＜0．即＜ ．

    这说明：x1＜ x2时，＞．也就是：自变量值增大了，对应的函数值反而变小了．

    即：当x＞0时，y随x的增大而减小．

    同理，当x＜0时，y随x的增大而减小．

    （1）试说明：反比例函数y＝  （k＞0）的图象关于原点对称．

       【运用推广】

    （2）分别写出二次函数y＝ax2 (a＞0，a为常数)的对称性和增减性，并进行说理．

    对称性：                                             ；

    增减性：                                            ．

    说理：

    （3）对于二次函数y＝ax2＋bx＋c (a＞0，a，b，c为常数)，请你从增减性的角度，简要解释为何当x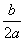＝— 时函数取得最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某市抽样调查了全市40个噪声测量点在某时刻的噪声声级（单位：dB），将调查的数

    据进行处理（设所测数据是正整数），得频数分布表如下：

    组  别

    噪声声级分组

    频  数

    频  率

    1

    44.5——59.5

    4

    0.1

    2

    59.5——74.5

    8

    0.2

    3

    74.5——89.5

    10

    0.25

    4

    89.5——104.5

    b

    c

    5

    104.5——119.5

    6

    0.15

    合 计

    40

    1.00

    则第四小组的频率c =_________．

    查看答案和解析>>

    同步练习册答案