练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    平面上有7条不同的直线，如果其中任何三条直线都不共点，

    （1）请画出满足上述条件的一个图形，并数出图形中各直线之间的交点个数；

    （2）请再画出各直线之间的交点个数不同的图形（至少两个）；

    （3）你能否画出各直线之间的交点个数为n的图形，其中n分别为6，21，157；

    （4）请尽可能多地画出各直线之间的交点个数不同的图形，从中你能发现什么规律？

     

    答案：
    解析：

    		提示：（1）、（2）略

    （3）当n=6时，必须使7条直线中有6条互相平行，另一条直线与这些平行线相交（如图1）；当n=21时，你必须使7条直线中的每两条都相交（即无任何两条平行）（如图2），这样所得的交点个数为6´7=21；当n=15时，作如图3的图形．

    （4）当我们给出较多的答案时，从较多的图形中，可以总结出以下一些规律：

    ①当7条直线都相互平行时，交点的个数是零，这时交点的个数最少；

    ②当7条直线每两条均相交时，交点的个数为21，这时交点的个数最多；

    ③设交点的个数为n，则0£n£21；

    ④n的大小直接取决于7条直线中相互平行的直线的数量，而7条直线中互相平行的直线有多种情形．

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    、阅读下列材料并填空。平面上有n个点（n≥2）且任意三个点不在同一条直线上，过这些点作直线，一共能作出多少条不同的直线？
    ①分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线……
    ②归纳：考察点的个数和可连成直线的条数发现：如下表
    点的个数
    		可作出直线条数
    2
    		1=
    3
    		3=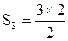
    4
    		6=
    5
    		10=
    ……
    		……
    n

    ③推理：平面上有n个点，两点确定一条直线。取第一个点A有n种取法，取第二个点B有（n－1）种取法，所以一共可连成n(n-1)条直线，但AB与BA是同一条直线，故应除以2；即
    ④结论：
    试探究以下几个问题：平面上有n个点（n≥3），任意三个点不在同一条直线上，过任意三个点作三角形，一共能作出多少不同的三角形？
    （1）分析：
    当仅有3个点时，可作出      个三角形；
    当仅有4个点时，可作出      个三角形；
    当仅有5个点时，可作出      个三角形；
    ……
    （2）归纳：考察点的个数n和可作出的三角形的个数，发现：（填下表）
    点的个数
    		可连成三角形个数
    3
    		 
    4
    		 
    5
    		 
    ……
    		 
    n
    		 
     
    (3)推理：                             
    （4）结论：

    查看答案和解析>>

    科目：初中数学 来源：2012届河南省虞城县营盘中学中考模拟三数学卷（带解析） 题型：解答题

    阅读下列材料并填空。平面上有n个点（n≥2）且任意三个点不在同一条直线上，过这些点作直线，一共能作出多少条不同的直线？
    （1）分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线……
    （2）归纳：考察点的个数和可连成直线的条数发现：如下表

    点的个数
    		可作出直线条数
    2
    		1=
    3
    		3=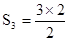
    4
    		6=
    5
    		10=
    ……
    		……
    n

    (3)推理：平面上有n个点，两点确定一条直线。取第一个点A有n种取法，取第二个点B有（n－1）种取法，所以一共可连成n(n-1)条直线，但AB与BA是同一条直线，故应除以2；即
    （4）结论：
    试探究以下几个问题：平面上有n个点（n≥3），任意三个点不在同一条直线上，过任意三个点作三角形，一共能作出多少不同的三角形？
    （1）分析：
    当仅有3个点时，可作出      个三角形；
    当仅有4个点时，可作出      个三角形；
    当仅有5个点时，可作出      个三角形；
    ……
    （2）归纳：考察点的个数n和可作出的三角形的个数，发现：（填下表）
    点的个数
    		可连成三角形个数
    3
    		 
    4
    		 
    5
    		 
    ……
    		 
    n
    		 
    (3)推理：                             （4）结论：

    查看答案和解析>>

    科目：初中数学 来源：北京四中2011年中考数学全真模拟11.doc 题型：填空题

    、阅读下列材料并填空。平面上有n个点（n≥2）且任意三个点不在同一条直线上，过这些点作直线，一共能作出多少条不同的直线？
    ①分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线……
    ②归纳：考察点的个数和可连成直线的条数发现：如下表

    点的个数
    		可作出直线条数
    2
    		1=
    3
    		3=
    4
    		6=
    5
    		10=
    ……
    		……
    n

    ③推理：平面上有n个点，两点确定一条直线。取第一个点A有n种取法，取第二个点B有（n－1）种取法，所以一共可连成n(n-1)条直线，但AB与BA是同一条直线，故应除以2；即
    ④结论：
    试探究以下几个问题：平面上有n个点（n≥3），任意三个点不在同一条直线上，过任意三个点作三角形，一共能作出多少不同的三角形？
    （1）分析：
    当仅有3个点时，可作出      个三角形；
    当仅有4个点时，可作出      个三角形；
    当仅有5个点时，可作出      个三角形；
    ……
    （2）归纳：考察点的个数n和可作出的三角形的个数，发现：（填下表）
    点的个数
    		可连成三角形个数
    3
    		 
    4
    		 
    5
    		 
    ……
    		 
    n
    		 
     
    (3)推理：                             
    （4）结论：

    查看答案和解析>>

    科目：初中数学 来源：2012年安徽省中考数学模拟试卷（二十）（解析版） 题型：解答题

    阅读下列材料并填空．
    平面上有n个点（n≥2）且任意三个点不在同一条直线上，过其中的每两点画直线，一共能作出多少条不同的直线？
    ①分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线…
    ②归纳：考察点的个数和可连成直线的条数Sn发现：如下表
    点的个数可作出直线条数
    21=S2=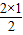
    33=S3=
    46=S4=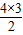
    510=S5=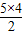
    ……
    nSn=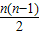
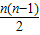    ③推理：平面上有n个点，两点确定一条直线．取第一个点A有n种取法，取第二个点B有（n-1）种取法，所以一共可连成n（n-1）条直线，但AB与BA是同一条直线，故应除以2；即Sn=④结论：Sn=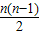试探究以下几个问题：平面上有n个点（n≥3），任意三个点不在同一条直线上，过任意三个点作三角形，一共能作出多少不同的三角形？
    （1）分析：
    当仅有3个点时，可作出______个三角形；
    当仅有4个点时，可作出______个三角形；
    当仅有5个点时，可作出______个三角形；
    …
    （2）归纳：考察点的个数n和可作出的三角形的个数Sn，发现：（填下表）
    点的个数可连成三角形个数
    3
    4
    5
    …
    n
    （3）推理：
    （4）结论：

    查看答案和解析>>

    科目：初中数学 来源：2003年甘肃省中考数学试卷（2）（解析版） 题型：解答题

    （2003•甘肃）阅读以下材料并填空．
    平面上有n个点（n≥2），且任意三个点不在同一直线上，过这些点作直线，一共能作出多少条不同的直线？
    （1）分析：当仅有两个点时，可连成1条直线；
    当有3个点时，可连成3条直线；
    当有4个点时，可连成6条直线；
    当有5个点时，可连成10条直线；
    …
    （2）归纳：考察点的个数n和可连成直线的条数Sn，发现：
    （3）推理：平面上有n个点，两点确定一条直线．取第一个点A有n种取法，取第二个点B有（n-1）种取法，所以一共可连成n（n-1）条直线，但AB与BA是同一条直线，故应除以2，即．
    （4）结论：．
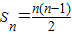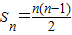    点的个数可连成直线条数
    2 l=S2=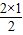
    33=S3=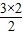
    4 6=S4=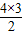
    5 10=S5=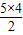
    ……
    n Sn=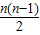
    试探究以下问题：
    平面上有n（n≥3）个点，任意三个点不在同一直线上，过任意三点作三角形，一共能作出多少不同的三角形？
    ①分析：
    当仅有3个点时，可作______个三角形；
    当有4个点时，可作______个三角形；
    当有5个点时，可作______个三角形；
    …
    ②归纳：考察点的个数n和可作出的三角形的个数Sn，发现：
    点的个数可连成三角形个数
    3 
    4 
    5 
    ……
    n 
    ③推理：______
    取第一个点A有n种取法，
    取第二个点B有（n-1）种取法，
    取第三个点C有（n-2）种取法，
    但△ABC、△ACB、△BAC、△BCA、△CAB、△CBA是同一个三角形，故应除以6．
    ④结论：______．

    查看答案和解析>>

    同步练习册答案