
【题目】问题探究:已知平行四边形![]() 的面积为
的面积为![]() ,
,![]() 是
是![]() 所在直线上一点.
所在直线上一点.
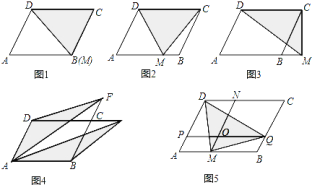
![]() 如图
如图![]() :当点
:当点![]() 与
与![]() 重合时,
重合时,![]() ________;
________;
![]() 如图
如图![]() ,当点
,当点![]() 与
与![]() 与
与![]() 均不重合时,
均不重合时,![]() ________;
________;
![]() 如图
如图![]() ,当点
,当点![]() 在
在![]() (或
(或![]() )的延长线时,
)的延长线时,![]() ________.
________.
拓展推广:如图![]() ,平行四边形
,平行四边形![]() 的面积为
的面积为![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 延长线上两点,连接
延长线上两点,连接![]() 、
、![]() 、
、![]() 、
、![]() ,求出图中阴影部分的面积,并说明理由.
,求出图中阴影部分的面积,并说明理由.
实践应用:如图是一平行四边形绿地![]() ,
,![]() 、
、![]() 分别平行于
分别平行于![]() 、
、![]() ,它们相交于点
,它们相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,现进行绿地改造,在绿地内部作一个三角形区域
,现进行绿地改造,在绿地内部作一个三角形区域![]() (连接
(连接![]() 、
、![]() 、
、![]() ,图中阴影部分)种植不同的花草,求出三角形区域的面积.
,图中阴影部分)种植不同的花草,求出三角形区域的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;拓展推广:阴影部分的面积
;拓展推广:阴影部分的面积![]() ;实践应用:三角形区域的面积
;实践应用:三角形区域的面积![]() .
.
【解析】
(1)平行四边形的面积等于底乘以高,设平行四边形ABCD的高为h, △DCM边CD的高也为h,由题S平行四边形ABCD=CD×h,S△DCM=![]() CD×h=
CD×h=![]() S平行四边形ABCD=50;
S平行四边形ABCD=50;
(2)由(1)同理可得S△DCM =50;
(3)由(1)同理可得S△DCM =50;
拓展推广:由(1)的结论可得S△ADF=![]() a, S△ABE=
a, S△ABE=![]() a,由此即可得阴影部分的面积;
a,由此即可得阴影部分的面积;
应用,由推广的结论,有![]() ,
,![]() ,
,![]() ,由此即可求出三角形区域的面积.
,由此即可求出三角形区域的面积.
![]() 设平行四边形ABCD的边CD上的高为h,则△DCM边CD的高也为h,
设平行四边形ABCD的边CD上的高为h,则△DCM边CD的高也为h,
∵S平行四边形ABCD=CD×h,则平行四边形![]() 的面积
的面积![]() ,
,
![]() ;
;
![]() 与
与![]() 同理可得
同理可得![]() ;
;
![]() 与
与![]() 同理可得
同理可得![]() ;
;
拓展推广:
根据![]() 的结论,
的结论,![]() ,
,
![]() ,
,
∴阴影部分的面积![]() ;
;
实践应用:
根据前面信息,![]() ,
,
![]() ,
,
![]() ,
,
∴三角形区域的面积![]() .
.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,线段AB是直线y=4x+2的一部分,点A是直线与y轴的交点,点B的纵坐标为6,曲线BC是双曲线y=![]() 的一部分,点C的横坐标为6,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线.点P(2017,m)与Q(2020,n)均在该波浪线上,分别过P、Q两点向x轴作垂线段,垂足为点D和E,则四边形PDEQ的面积是( )
的一部分,点C的横坐标为6,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线.点P(2017,m)与Q(2020,n)均在该波浪线上,分别过P、Q两点向x轴作垂线段,垂足为点D和E,则四边形PDEQ的面积是( )

A. 10 B. ![]() C.
C. ![]() D. 15
D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AD=4,BC=12,点E是BC的中点.点P、Q分别是边AD、BC上的两点,其中点P以每秒个1单位长度的速度从点A运动到点D后再返回点A,同时点Q以每秒2个单位长度的速度从点C出发向点B运动.当其中一点到达终点时停止运动.当运动时间t为_____秒时,以点A、P,Q,E为顶点的四边形是平行四边形.
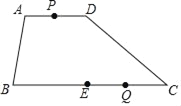
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,同时点
的速度移动,同时点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为
的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为![]() 秒,
秒,
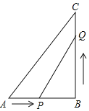
![]() 求几秒后,
求几秒后,![]() 的面积等于
的面积等于![]() ?
?
![]() 求几秒后,
求几秒后,![]() 的长度等于
的长度等于![]() ?
?
![]() 运动过程中,
运动过程中,![]() 的面积能否等于
的面积能否等于![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
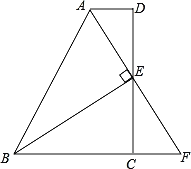
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点 ![]() 在
在 ![]() 轴负半轴上,顶点
轴负半轴上,顶点![]() 在
在![]() 轴正半轴上,顶点
轴正半轴上,顶点 ![]() 在第一象限,线段
在第一象限,线段 ![]() ,
,![]() 的长是一元二次方程
的长是一元二次方程 ![]() 的两根,
的两根,![]() ,
,![]() .
.
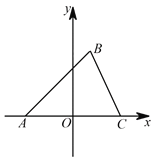
(1)直接写出点![]() 的坐标 点 C 的坐标 ;
的坐标 点 C 的坐标 ;
(2)若反比例函数![]() 的图象经过点
的图象经过点![]() ,求
,求 ![]() 的值;
的值;
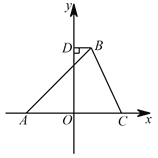
(3)如图过点![]() 作
作![]() 轴于点
轴于点 ![]() ;在
;在![]() 轴上是否存在点
轴上是否存在点 ![]() ,使以
,使以![]() ,
,![]() ,
,![]() 为顶点的三角形与以
为顶点的三角形与以![]() ,
,![]() ,
,![]() 为顶点的三角形相似?若存在,直接写出满足条件的点
为顶点的三角形相似?若存在,直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成后面题目.
0°-360°间的角的三角函数
在初中,我们学习过锐角的正弦、余弦、正切和余切四种三角函数,即在图1所示的直角三角形ABC,∠A是锐角,那么sinA=![]() ,cosA=
,cosA=![]() ,tanA=
,tanA=![]() ,cotA=
,cotA=![]()
为了研究需要,我们再从另一个角度来规定一个角的三角函数的意义:
设有一个角α,我们以它的顶点作为原点,以它的始边作为x轴的正半轴ox,建立直角坐标系(图2),在角α的终边上任取一点P,它的横坐标是x,纵坐标是y,点P和原点(0,0)的距离为r=![]() (r总是正的),然后把角α的三角函数规定为:sinα=
(r总是正的),然后把角α的三角函数规定为:sinα=![]() ,cosα=
,cosα=![]() ,tanα=
,tanα=![]() ,cotα=
,cotα=![]()
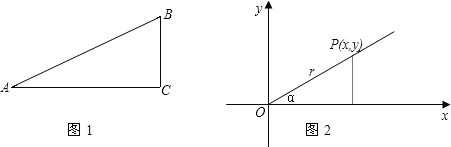
我们知道,图1的四个比值的大小与角A的大小有关,而与直角三角形的大小无关,同样图2中四个比值的大小也仅与角α的大小有关,而与点P在角α的终边位置无关.
比较图1与图2,可以看出一个角的三角函数的意义的两种规定实际上是一样的,根据第二种定义回答下列问题.
(1)若90°<α<180°,则角α的三角函数值sinα、cosα、tanα、cotα,其中取正值的是哪几个?
(2)若角α的终边与直线y=2x重合,求sinα+cosα的值.
(3)若角α是钝角,其终边上一点P(x,![]() ),且cosα=
),且cosα=![]() x,求tanα的值.
x,求tanα的值.
(4)若0°≤α≤90°,求sinα+cosα的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2018年平均每天的垃圾处理量为40万吨/天,2019年平均每天的垃圾排放量比2018年平均每天的垃圾排放量多100万吨;2019年平均每天的垃圾处理量是2018年平均每天的垃圾处理量的2. 5倍. 若2019年平均每天的垃圾处理率是2018年平均每天的垃圾处理率的1. 25倍.
(注:![]() )
)
(1)求该市2018年平均每天的垃圾排放量;
(2)预计该市2020年平均每天的垃圾排放量比2019年平均每天的垃圾排放量增加![]() . 如果按照创卫要求“城市平均每天的垃圾处理率不低于
. 如果按照创卫要求“城市平均每天的垃圾处理率不低于![]() ”,那么该市2020年平均每天的垃圾处理量在2019年平均每天的垃圾处理量的基础上,至少还需要増加多少万吨才能使该市2020年平均每天的垃圾处理率符合创卫的要求?
”,那么该市2020年平均每天的垃圾处理量在2019年平均每天的垃圾处理量的基础上,至少还需要増加多少万吨才能使该市2020年平均每天的垃圾处理率符合创卫的要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com