
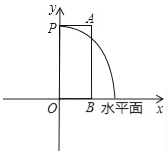
【题目】某市人民广场上要建一个圆形的喷水池,并在水池中央垂直安装一个柱子OP,柱子顶端P处装上喷头,由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP=3米,喷出的水流的最高点A距水平面的高度是4米,离柱子OP的距离为1米.
(1)求这条抛物线的解析式;
(2)若不计其它因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外.
【答案】(1)y=﹣(x﹣1)2+4;(2)3.
【解析】试题分析: (1)根据题意可设解析式为顶点式形式,由A、P两点坐标求解析式;
(2)求水池半径即时求当y=0时x的值.
试题解析:
解:(1)设这条抛物线解析式为y=a(x+m)2+k
由题意知:顶点A为(1,4),P为(0,3)
∴4=k,3=a(0﹣1)2+4,a=﹣1.
所以这条抛物线的解析式为y=﹣(x﹣1)2+4.
(2)令y=0,则0=﹣(x﹣1)2+4,
解得x1=3,x2=﹣1
所以若不计其它因素,水池的半径至少3米,才能使喷出的水流不至于落在池外.
点睛: 本题考查二次函数的性质、配方法等知识,解题的关键是学会构建二次函数解决实际问题,属于中考常考题型.


科目:初中数学 来源: 题型:
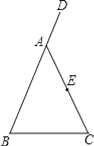
【题目】如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
(1)利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);
(2)试判断AF与BC有怎样的位置关系与数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
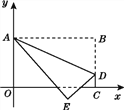
【题目】如图,将长方形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将长方形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当m=3时,点B的坐标为_________,点E的坐标为_________;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
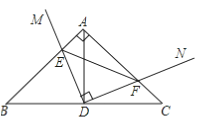
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
A. ①②④ B. ②③④
C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,某校积极开展拓展性课程建设,设计开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程。为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):

根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数;
(2)将条形图补充完整;
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四种沿![]() 折叠的方法中,不一定能判定纸带两条边线
折叠的方法中,不一定能判定纸带两条边线![]() ,
, ![]() 互相平行的是( ).
互相平行的是( ).

A. 如图![]() ,展开后测得
,展开后测得![]()
B. 如图![]() ,展开后测得
,展开后测得![]()
C. 如图![]() ,测得
,测得![]()
D. 如图![]() ,展开后再沿
,展开后再沿![]() 折叠,两条折痕的交点为
折叠,两条折痕的交点为![]() ,测得
,测得![]() ,
, ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l外有不重合的两点A、B.在直线l上求一点C,使得![]() 的长度最短,作法为:①作点B关于直线l的对称点B'.②连接AB'交直线l于点C,则点C即为所求.在解决这个问题时,没有用到的知识点是( )
的长度最短,作法为:①作点B关于直线l的对称点B'.②连接AB'交直线l于点C,则点C即为所求.在解决这个问题时,没有用到的知识点是( )

A. 线段的垂直平分线性质 B. 两点之间线段最短
C. 三角形两边之和大于第三边 D. 角平分线的性质
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货11吨;用1辆A型车和2辆B型车载满货物一次可运货13吨.根据以上信息, 解答下列问题:
(1)1辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)某物流公司现有31吨货物,计划同时租用A型车![]() 辆,B型车
辆,B型车![]() 辆,一次运完,且恰好每辆车都载满货物请用含有
辆,一次运完,且恰好每辆车都载满货物请用含有![]() 的式子表示
的式子表示![]() ,并帮该物流公司设计租车方案;
,并帮该物流公司设计租车方案;
(3)在(2)的条件下,若A型车每辆需租金500元/次,B型车每辆需租金600元/次.请选出最省钱的租车方案,并求出最少租车费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com