
【题目】如图,已知△ABC是等边三角形,D是边AC的中点,连接BD,EC⊥BC于点C,CE=BD.求证:△ADE是等边三角形.

【答案】详见解析.
【解析】
利用△ABC是等边三角形,D为边AC的中点,求得∠ADB=90°,再用SAS证明△CBD≌△ACE,推出AE=CD=AD,∠AEC=∠BDC=90°,根据直角三角形斜边上中线性质求出DE=AD,即可得出答案.
证明:∵△ABC是等边三角形,D为边AC的中点,
∴BD⊥AC,即∠ADB=90°,
∵EC⊥BC,
∴∠BCE=90°,
∴∠DBC+∠DCB=90°,∠ECD+∠BCD=90°,
∴∠ACE=∠DBC,
∵在△CBD和△ACE中
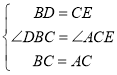
∴△CBD≌△ACE(SAS),
∴CD=AE,∠AEC=∠BDC=90°,
∵D为边AC的中点,∠AEC=90°,
∴AD=DE,
∴AD=AE=DE,
即△ADE是等边三角形,


科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需 分钟到达终点B.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为线段AB上一点,△ACD、△CBE都是等边三角形,AE交DC于点M,BD交CE于点N,下列说法一定正确的是________(请把你认为正确答案的序号填在横线上)
①AE=BD;②∠AEC=∠BDC;③AM=DN;④DM=CN;⑤CM=MN;⑥MN∥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD,延长AD到E,使DE=AD,连接BE与DC交于O点.

(1)求证:△BOC≌△EOD;
(2)当△ABE满足什么条件时,四边形BCED是菱形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战
士们离营地的距离![]() 与时间
与时间![]() 之间函数关系的是( )
之间函数关系的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).
(1)请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在图中y轴右侧,画出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点C1在边BC上,将△C1CD绕点D顺时针旋转90°得到△A1AD.A1F平分∠BA1C1,交BD于点F,过点F作FE⊥A1C1,垂足为E,当A1E=3,C1E=2时,则BD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需![]() 天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需
天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需![]() 天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);

(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com