
【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法。
问题提出:求边长分别为![]() 的三角形面积。
的三角形面积。
问题解决:在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为![]() 的格点三角形△ABC(如图①),AB=
的格点三角形△ABC(如图①),AB=![]() 是直角边为1和2的直角三角形斜边,BC=
是直角边为1和2的直角三角形斜边,BC=![]() 是直角边分别为1和3的直角三角形的斜边,AC=
是直角边分别为1和3的直角三角形的斜边,AC=![]() 是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。
是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。

(1)请直接写出图①中△ABC的面积为_______________ 。
(2)类比迁移:求边长分别为![]() 的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
科目:初中数学 来源: 题型:
【题目】为验证“掷一个质地均匀的骰子,向上的点数为偶数的概率是0.5”,下列模拟实验中,不科学的是( )
A. 袋中装有1个红球一个绿球,它们除颜色外都相同,计算随机摸出红球的概率
B. 用计算器随机地取不大于10的正整数,计算取得奇数的概率
C. 随机掷一枚质地均匀的硬币,计算正面朝上的概率
D. 如图,将一个可以自由旋转的转盘分成甲、乙、丙3个相同的扇形,转动转盘任其自由停止,计算指针指向甲的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
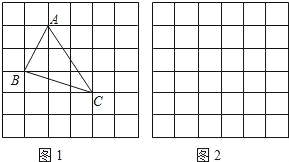
(1)请你利用上述方法求出△ABC的面积.
(2)在图2中画△DEF,DE、EF、DF三边的长分别为![]() 、
、![]() 、
、![]()
①判断三角形的形状,说明理由.
②求这个三角形的面积.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:
(x-1)(x+1)=x2-1, (x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1, (x-1)(x4+x3+x2+x+1)=x5-1,
……
(1)试写出第五个等式;
(2)试求26+25+24+23+22+2+1的值;
(3)判断22 017+22 016+22 015+…+22+2+1的值的个位数字是几.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-23+![]() (2018+3)0-
(2018+3)0-![]() ; (2)992-69×71;
; (2)992-69×71;
(3) ![]() ÷(-3xy); (4)(-2+x)(-2-x);
÷(-3xy); (4)(-2+x)(-2-x);
(5)(a+b-c)(a-b+c); (6)(3x-2y+1)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是小王和小李在一次跑步比赛中的时间和路程图.
(1)这次比赛的路程是_______米;
(2)小王的平均速度是_________米/秒;
(3)他们先到达终点的是_______;
(4)小李跑步的路程![]() (米)与时间
(米)与时间![]() (秒)的函数关系式是_________.
(秒)的函数关系式是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 是线段
是线段![]() 所在平面内任意一点,分别以
所在平面内任意一点,分别以![]() 、
、![]() 为边,在
为边,在![]() 同侧作等边
同侧作等边![]() 和等边
和等边![]() ,联结
,联结![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图1,当点![]() 在线段
在线段![]() 上移动时,线段
上移动时,线段![]() 与
与![]() 的数量关系是:________;
的数量关系是:________;
(2)如图2,当点![]() 在直线
在直线![]() 外,且
外,且![]() ,仍分别以
,仍分别以![]() 、
、![]() 为边,在
为边,在![]() 同侧作等边
同侧作等边![]() 和等边
和等边![]() ,联结
,联结![]() 、
、![]() 交于点
交于点![]() .(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时
.(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时![]() 是否随
是否随![]() 的大小发生变化?若变化,写出变化规律,若不变,请求出
的大小发生变化?若变化,写出变化规律,若不变,请求出![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,联结![]() ,求证:
,求证: ![]() 平分
平分![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边AB在数轴上,数轴上点A表示的数为﹣1,正方形ABCD的面积为16.
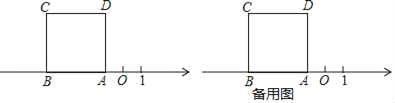
(1)数轴上点B表示的数为 ;
(2)将正方形ABCD沿数轴水平移动,移动后的正方形记为A′B′C′D′,移动后的正方形A′B′C′D′与原正方形ABCD重叠部分的面积为S.
①当S=4时,画出图形,并求出数轴上点A′表示的数;
②设正方形ABCD的移动速度为每秒2个单位长度,点E为线段AA′的中点,点F在线段BB′上,且BF=![]() BB′.经过t秒后,点E,F所表示的数互为相反数,直接写出t的值.
BB′.经过t秒后,点E,F所表示的数互为相反数,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
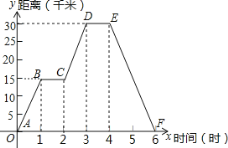
(1)根据图象回答:小明到达离家最远的地方需 小时,
(2)小明出发两个半小时离家 千米.
(3)小明出发 小时离家12千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com