练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】作图题：（不写作法，但必须保留作图痕迹）

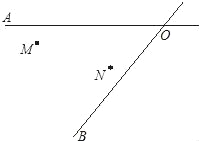
    如图：某地有两所大学和两条相交叉的公路，（点M，N表示大学，AO，BO表示公路）．现计划修建一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等．你能确定仓库P应该建在什么位置吗？在所给的图形中画出你的设计方案．

    【答案】见解析

    【解析】

    先连接MN，根据线段垂直平分线的性质作出线段MN的垂直平分线DE，再作出∠AOB的平分线OF，DE与OF相交于P点，则点P即为所求．

    解：如图所示：

    （1）连接MN，分别以M、N为圆心，以大于MN为半径画圆，两圆相交于DE，连接DE，则DE即为线段MN的垂直平分线；

    （2）以O为圆心，以任意长为半径画圆，分别交OA、OB于G、H，再分别以G、H为圆心，以大于GH为半径画圆，两圆相交于F，连接OF，则OF即为∠AOB的平分线（或∠AOB的外角平分线）；

    （3）DE与OF相交于点P，则点P即为所求．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）如图，若，将点在内部，∠，∠，∠满足的数量关系是　 　，并说明理由．

    (2)在如图1中，将直线绕点逆时针方向旋转一定角度交直线于点，如图2，利用（1）中的结论（可以直接套用），求∠﹑∠﹑∠﹑∠之间有何数量关系？

    (3)科技活动课上，雨轩同学制作了一个图（3）的“飞旋镖”，经测量发现∠＝°，∠＝°，则∠与∠的数量关系是 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A、B在反比例函数 的图象上，且点A、B的横坐标分别为a、2a（a＞0），AC⊥x轴，垂足为C，且△AOC的面积为2，

    （1）求该反比例函数的解析式；
    （2）求△AOB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AE交BC于点D，∠C=∠E，AD：DE=3：5，AE=8，BD=4，求DC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，﹣1），B（﹣1，1），C（0，﹣2）．

    （1）写出点B关于坐标原点O对称的点B1的坐标；
    （2）将△ABC绕点C顺时针旋转90°，画出旋转后得到的△A1B1C；
    （3）求过点B1的正比例函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】乘法公式的探究及应用.

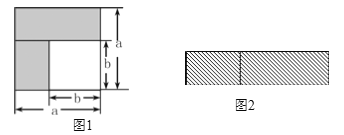
    (1)如图1，可以求出阴影部分的面积是 (写成两数平方差的形式)；

    (2)如图2，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是 ，长是 ，面积是 (写成多项式乘法的形式)；

    (3)比较图1、图2两图的阴影部分面积，可以得到乘法公式 (用式子表达)；

    (4)运用你所得到的公式，计算下列各题：

    ①(2m+n-p)(2m-n+p)；②10.3×9.7.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补．

    （1）试判断直线AB与直线CD的位置关系，并说明理由；

    （2）如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；

    （3）如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK＝∠HPK，作PQ平分∠EPK，问∠HPQ的大小是否发生变化？若不变，请求出其值；若变化，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（背景介绍）勾股定理是几何学中的明珠，充满着魅力．千百年来，人们对它的证明趋之若骛，其中有著名的数学家，也有业余数学爱好者．向常春在1994年构造发现了一个新的证法．

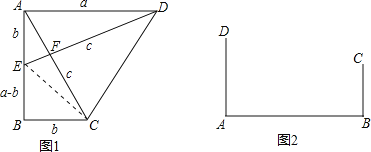
    （小试牛刀）把两个全等的直角三角形如图1放置，其三边长分别为a、b、c．显然，∠DAB=∠B=90°，AC⊥DE．请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积，再探究这三个图形面积之间的关系，可得到勾股定理：

    S梯形ABCD= ，

    S△EBC= ，

    S四边形AECD= ，

    则它们满足的关系式为 ，经化简，可得到勾股定理．

    （知识运用）（1）如图2，铁路上A、B两点（看作直线上的两点）相距40千米，C、D为两个村庄（看作两个点），AD⊥AB，BC⊥AB，垂足分别为A、B，AD=25千米，BC=16千米，则两个村庄的距离为 千米（直接填空）；

    （2）在（1）的背景下，若AB=40千米，AD=24千米，BC=16千米，要在AB上建造一个供应站P，使得PC=PD，请用尺规作图在图2中作出P点的位置并求出AP的距离．

    （知识迁移）借助上面的思考过程与几何模型，求代数式最小值（0＜x＜16）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

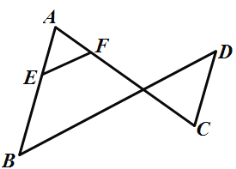
    【题目】如图，已知，．说明的理由．

    解：∵（已知），

    ∴________//________（_______________）

    ∴（_______________）

    ∵（________），

    ∴（_______________）

    ∵（己证），

    ∴（_______________）．

    查看答案和解析>>

    同步练习册答案