
 如图,边长都为1的正方形AEFG与正方形ABCD,正方形AEFG绕顶点A旋转一周,在此旋转过程中,线段DF的长可取的整数值为1和2.
如图,边长都为1的正方形AEFG与正方形ABCD,正方形AEFG绕顶点A旋转一周,在此旋转过程中,线段DF的长可取的整数值为1和2.  星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:解答题
A,B两点在数轴上的位置如图所示,其中点A对应的有理数为-4,且AB=10。动点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒(t>0)。

(1)当t=1时,AP的长为_________,点P表示的有理数为______;
(2)当PB=2时,求t的值;
(3)M为线段AP的中点,N为线段PB的中点. 在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长。
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
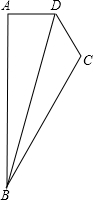 如图,四边形ABCD中,∠DAB=90°,AD=CD,∠BCD=∠CDA=120°,则$\frac{{S}_{△ABD}}{{S}_{△BDC}}$=$\frac{4}{3}$.
如图,四边形ABCD中,∠DAB=90°,AD=CD,∠BCD=∠CDA=120°,则$\frac{{S}_{△ABD}}{{S}_{△BDC}}$=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
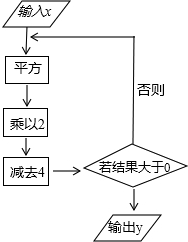 根据如图所示的程序计算.
根据如图所示的程序计算.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6÷(-$\frac{1}{4}$)×4=6×(-4)×4 | B. | 6÷(-$\frac{1}{4}$)×4=6×(-$\frac{1}{4}$)×4 | C. | 6÷(-$\frac{1}{4}$)×4=6÷(-$\frac{1}{4}$×4) | D. | 6÷(-$\frac{1}{4}$)×4=6×(-4)÷4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=BC,点D为AB中点,点E在BA的延长线上,过B作BF⊥EC交EC延长线于F,交DC延长线于G.
如图,在△ABC中,∠ACB=90°,AC=BC,点D为AB中点,点E在BA的延长线上,过B作BF⊥EC交EC延长线于F,交DC延长线于G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com