
已知,二次函数 的图象如图所示.
的图象如图所示.
(1)若二次函数的对称轴方程为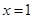 ,求二次函数的解析式;
,求二次函数的解析式;
(2)已知一次函数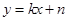 ,点
,点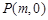 是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数
是x轴上的一个动点.若在(1)的条件下,过点P垂直于x轴的直线交这个一次函数的图象于点M,交二次函数 的图象于点N.若只有当1<m<
的图象于点N.若只有当1<m< 时,点M位于点N的上方,求这个一次函数的解析式;
时,点M位于点N的上方,求这个一次函数的解析式;
(3)若一元二次方程 有实数根,请你构造恰当的函数,根据图象直接写出
有实数根,请你构造恰当的函数,根据图象直接写出 的最大值.
的最大值.
(1) ;(2)
;(2) ;(3)
;(3)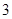 .
.
解析试题分析:(1)根据二次函数的对称轴可知二次函数的顶点坐标为(1,-3),二次函数与 轴的交点坐标为
轴的交点坐标为 ,即可根据待定系数法求得结果;
,即可根据待定系数法求得结果;
(2)由题意得一次函数的图象与二次函数的图象交点的横坐标分别为1和 ,即可得交点坐标为
,即可得交点坐标为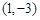 和
和 ,再根据待定系数法即可求得结果;
,再根据待定系数法即可求得结果;
(3)先构造恰当的函数,在根据图象的性质即可得到结果.
(1) 二次函数的对称轴方程为
二次函数的对称轴方程为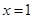 ,由二次函数的图象可知二次函数的顶点坐标为(1,-3),二次函数与
,由二次函数的图象可知二次函数的顶点坐标为(1,-3),二次函数与 轴的交点坐标为
轴的交点坐标为 ,
,
于是得到方程组
解方程得
二次函数的解析式为 ;
;
(2)由(1)得二次函数解析式为
依题意并结合图象可知,一次函数的图象与二次函数的图象交点的横坐标分别为1和
由此可得交点坐标为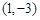 和
和
将交点坐标分别代入一次函数解析式 中
中
得
解得 
∴ 一次函数的解析式为 ;
;
(3)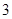 .
.
考点:二次函数的应用
点评:解答本题的关键是熟练掌握抛物线的对称性,同时正确运用待定系数法求函数关系式.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com