
【题目】如图,直线y=kx+b经过点A(5,0),B(1,4).
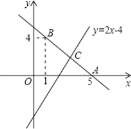
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4≥kx+b的解集.
科目:初中数学 来源: 题型:
【题目】已知, ![]() ,
, ![]() 与
与![]() 成正比例,
成正比例, ![]() 与
与![]() 成反比例,并且当
成反比例,并且当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
(![]() )求
)求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(![]() )当
)当![]() 时,求
时,求![]() 的值.
的值.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ,
, ![]() .
.
【解析】分析:(1)首先根据![]() 与x成正比例,
与x成正比例, ![]() 与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出
与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出![]() 和
和![]() 与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
本题解析:
(![]() )设
)设![]() ,
, ![]() ,
,
则![]() ,
,
∵当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∴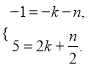
解得, ![]() ,
,
∴![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]() .
.
(![]() )把
)把![]() 代入
代入![]() 得,
得,
![]() ,
,
解得: ![]() ,
, ![]() .
.
点睛:本题考查了用待定系数法求反比例函数的解析式:(1)设出含有待定系数的反比例函数解析式y=kx(k为常数,k≠0);(2)把已知条件(自变量与对应值)代入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.
【题型】解答题
【结束】
24
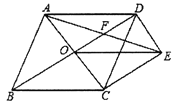
【题目】如图,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若菱形![]() 的边长为2,
的边长为2, ![]() .求
.求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线CD//EF ,点A、B分别在直线CD与EF上。P为两平行线间一点
(1)若∠DAP= 40° , ∠FBP=70°,求∠APB的度数是多少?
(2)直接写出∠DAP, ∠FBP, ∠APB之间有什么关系?
(3)利用(2)的结论解答:
①如图2, AP1、BP1,分别平分∠DAP,∠FBP,请你写出∠P与∠P1,的数量关系,并说明理由;
②如图3, AP2、 BP2分别平分∠CAP,∠EBP,若∠APB=β,求∠AP2B (用含β的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程a2x2+(2a-1)x+1=0有两个不相等的实数根x1,x2.(1)求a的取值范围;(2)是否存在实数a,使方程的两个实数根互为相反数?如果存在,求出a的值;如果不存在,说明理由.
解:(1)根据题意,得△=(2a-1)2-4a2>0,解得a<![]() .
.
∴当a<0时,方程有两个不相等的实数根.
(2)存在,如果方程的两个实数根x1,x2互为相反数,则x1+x2=-![]() =0 ①,
=0 ①,
解得a=![]() ,经检验,a=
,经检验,a=![]() 是方程①的根.
是方程①的根.
∴当a=![]() 时,方程的两个实数根x1与x2互为相反数.
时,方程的两个实数根x1与x2互为相反数.
上述解答过程是否有错误?如果有,请指出错误之处,并解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是正方形,点E、F分别是BC、CD边的中点,连结AE、BF交于点P,连结DP.
(1)求证:AE⊥BF.
(2)求证:PD=AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
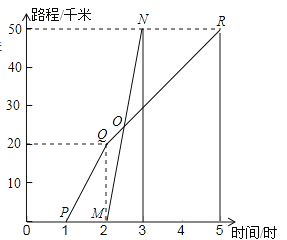
【题目】如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按相同路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S和时间t的关系.象回答下列问题:
(1)甲和乙哪一个出发的更早?早出发多长时间?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?
(4)请你根据图象上的数据,求出乙出发后多长时间追上甲?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了争创全国文明卫生城市,优化城市环境,某市公交公司决定购买10辆全新的混合动力公交车,现有![]() 两种型号,它们的价格及年省油量如下表:
两种型号,它们的价格及年省油量如下表:
型 号 |
|
|
价格(万元/辆) |
|
|
年省油量(万升/辆) | 2.4 | 2 |
经调查,购买一辆![]() 型车比购买一辆
型车比购买一辆![]() 型车多20万元,购买2辆
型车多20万元,购买2辆![]() 型车比购买3辆
型车比购买3辆![]() 型车少60万元.
型车少60万元.
(1)请求出![]() 和
和![]() 的值;
的值;
(2)若购买这批混合动力公交车(两种车型都要有), 每年能节省的油量不低于22.4万升,请问有几种购车方案?(不用一一列出)请求出最省钱的购车方案所需的车款.
查看答案和解析>>
科目:初中数学 来源: 题型:
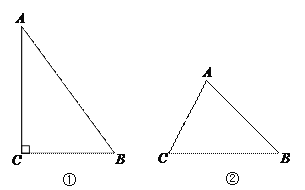
【题目】在△ABC中,D为BC边上一点.
(1)如图①,在Rt△ABC中,∠C=90°,将△ABC沿着AD折叠,点C落在AB边上.请用直尺和圆规作出点D(不写作法,保留作图痕迹);
(2)如图②,将△ABC沿着过点D的直线折叠,点C落在AB边上的E处.
①若DE⊥AB,垂足为E,请用直尺和圆规作出点D(不写作法,保留作图痕迹);
②若AB=![]() ,BC=3,∠B=45°,求CD的取值范围.
,BC=3,∠B=45°,求CD的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com