
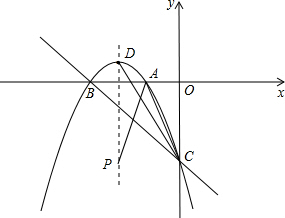
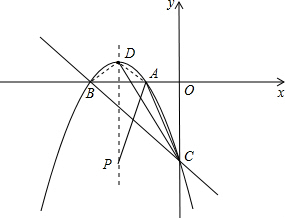
 (2012•合川区模拟)如图,二次函数y=-x2+bx+c的图象与x轴交于点B(-3,0),与y轴交于点C(0,-3).
(2012•合川区模拟)如图,二次函数y=-x2+bx+c的图象与x轴交于点B(-3,0),与y轴交于点C(0,-3).
|
|
|
|
| 32+32 |
| 2 |
| 12+[-1-(-2)]2 |
| 2 |
| 1 |
| (-1)-(-2) |
| DP |
| BC |
| AD |
| AB |
| DP | ||
3
|
| ||
| 2 |
| 1 |
| -2-(-3) |
| 12+[-2-(-3)]2 |
| 2 |
| BD |
| BC |
| ||
3
|
| 1 |
| 3 |
| AO |
| CO |
| 1 |
| 3 |


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
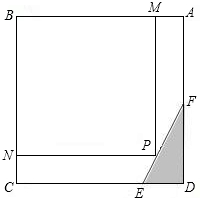 (2012•合川区模拟)如图,规格为60cm×60cm的正方形地砖在运输过程中受损,断去一角,量得AF=30cm,CE=45cm,现准备从五边形地砖ABCDE上截出一个面积为S的矩形地砖PMBN,则S最大值是( )
(2012•合川区模拟)如图,规格为60cm×60cm的正方形地砖在运输过程中受损,断去一角,量得AF=30cm,CE=45cm,现准备从五边形地砖ABCDE上截出一个面积为S的矩形地砖PMBN,则S最大值是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com