
【题目】(1)(发现)如图1,在![]() 中,
中,![]() 分别交
分别交![]() 于
于![]() ,交
,交![]() 于
于![]() .已知
.已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
思考发现,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,构造
,构造![]() ,经过推理和计算能够使问题得到解决(如图2).
,经过推理和计算能够使问题得到解决(如图2).

请回答:![]() 的值为______.
的值为______.
(2)(应用)如图3,在四边形![]() 中,
中,![]() ,
,![]() 与
与![]() 不平行且
不平行且![]() ,对角线
,对角线![]() ,垂足为
,垂足为![]() .若
.若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
(3)(拓展)如图4,已知平行四边形![]() 和矩形
和矩形![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() ,
,![]() ,判断
,判断![]() 与
与![]() 的数量关系并证明.
的数量关系并证明.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由DE//BC,EF//DC,可证得四边形DCFE是平行四边形,求出DE=CF,DC=EF,由DC⊥BE,可得△BEF是直角三角形,利用勾股定理,求出BF的长即为BC+DE的值;
(2)同(1)做CE//DB,交AB延长线于点E,易证四边形DBEC是平行四边形,根据已知可证△DAB![]() △CBA(SAS),得AC=DB,等量代换,可得AC=CE,故△ACE是等腰直角三角形,AE=8,利用勾股定理,即可求得AC;
△CBA(SAS),得AC=DB,等量代换,可得AC=CE,故△ACE是等腰直角三角形,AE=8,利用勾股定理,即可求得AC;
(3)连接AE、CE,由四边形ABCD是平行四边形,四边形ABEF是矩形,易证得四边形DCEF是平行四边形,继而证得△ACE是等腰直角三角形,求出AC=![]() CE,而DF=CE,即可得出答案.
CE,而DF=CE,即可得出答案.
解:(1)∵DE//BC,EF//DC,
∴四边形DCFE是平行四边形,
∴DE=CF,DC=EF,
∴BC+ED=BC+CF=BF,
∵DC⊥BE,DC//EF,
∴∠BEF=90°,在Rt△BEF中,
∵BE=5,EF=DC=3,
∴BF=![]() =
=![]() .
.
故BC+DE=![]() .
.
(2)做CE//DB,交AB延长线于点E,

由(1)同理,可证得四边形DBEC是平行四边形,BE=DC=3,
在△DAB和△CBA中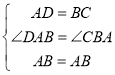 ,
,
∴△DAB![]() △CBA(SAS),
△CBA(SAS),
∴DB=AC,
∵四边形DBEC是平行四边形,DB=CE,
∴AC=CE,
∵AC⊥DB,
∴AC⊥CE,
∴△ACE是等腰直角三角形,
∵AE=AB+BE=AB+DC=5+3=8,
∴AC=![]() ,求得AC=
,求得AC=![]() .
.
故AC的长为![]() .
.
(3)AC=![]() DF;
DF;
证明:连接AE、CE,如图,
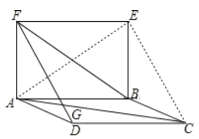
∵四边形ABCD是平行四边形,
∴AB//DC,
∵四边形ABEF是矩形,
∴AB//FE,BF=AE,
∴DC//FE,
∴四边形DCEF为平行四边形,
∴CE=DF,
∵四边形ABEF是矩形,
∴BF=AE,
∵BF=DF,
∴DF=CE,
∴AF=BE,
∵四边形ABCD是平行四边形,
∴AD=BC,
在△FAD和△EBC中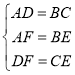 ,
,
∴△FAD![]() △EBC(SSS),
△EBC(SSS),
∴∠AFD=∠BEC,
∴∠FEB=∠EFA=90°,
∵∠EBF=60°,∠BFD=30°,
∴∠DFA=90°-30°-(90°-60°)=30°,
∴∠CEB=30°,
∴OE=OB,
∵∠EBF=60°,
∴∠BEA=∠EBF=60°,
∴∠AEC=60°+30°=90°,
即△AEC是等腰直角三角形,
∴AC=![]() CE,
CE,
∵DF=CE,
∴AC=![]() DF.
DF.
故AC与DF之间的数量关系是AC=![]() DF.
DF.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.

(1)求证:DF是⊙O的切线;
(2)若CF=2,DF=2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60(![]() +3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
+3)海里,在B处测得C在北偏东45°方向上,A处测得C在北偏西30°方向上,在海岸线AB上有一等他D,测得AD=100海里.
(1)分别求出AC,BC(结果保留根号)
(2)已知在灯塔D周围80海里范围内有暗礁群,在A处海监船沿AC前往C处盘看,图中有无触礁的危险?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2﹣10x+16=0的两个根,且抛物线的对称轴是直线x=﹣2.
(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出定义,若一个四边形中存在相邻两边的平方和等于任意一条对角线的平方,则称该四边形为勾股四边形.
(1)请在你学过的特殊四边形中,写出两种勾股四边形______、______;
(2)如图,将钝角△ABC绕点B顺时针旋转60°得到△DBE,连接AD、DC、CE,若∠DCE=90°.求证:四边形ABCD为勾股四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com