
【题目】【特例发现】如图1,在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB,AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.求证:EP=FQ.
【延伸拓展】如图2,在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB,AC为直角边,向△ABC外作Rt△ABE和Rt△ACF,射线GA交EF于点H.若AB=kAE,AC=kAF,请思考HE与HF之间的数量关系,并直接写出你的结论.
【深入探究】如图3,在△ABC中,G是BC边上任意一点,以A为顶点,向△ABC外作任意△ABE和△ACF,射线GA交EF于点H.若∠EAB=∠AGB,∠FAC=∠AGC,AB=kAE,AC=kAF,上一问的结论还成立吗?并证明你的结论.
【应用推广】在上一问的条件下,设大小恒定的角∠IHJ分别与△AEF的两边AE、AF分别交于点M、N,若△ABC为腰长等于4的等腰三角形,其中∠BAC=120°,且∠IHJ=∠AGB=θ=60°,k=2;
求证:当∠IHJ在旋转过程中,△EMH、△HMN和△FNH均相似,并直接写出线段MN的最小值(请在答题卡的备用图中补全作图).

【答案】(1)证明参见解析;(2)HE=HF;(3)成立,证明参见解析;(4)证明参见解析,MN最小值为1.
【解析】
试题分析:(1)特例发现:易证△AEP≌△BAG,△AFQ≌△CAG,即可求得EP=AG,FQ=AG,即可解题;(2)延伸拓展:过点E、F作射线GA的垂线,垂足分别为P、Q.易证△ABG∽△EAP,△ACG∽△FAQ,得到PE=![]() AG,FQ=
AG,FQ=![]() AG,∴PE=FQ,然后证明△EPH≌△FQH,即可得出HE=HF;(3)深入探究:判断△PEA∽△GAB,得到PE=
AG,∴PE=FQ,然后证明△EPH≌△FQH,即可得出HE=HF;(3)深入探究:判断△PEA∽△GAB,得到PE=![]() AG,△AQF∽△CGA,FQ=,得到FQ=
AG,△AQF∽△CGA,FQ=,得到FQ=![]() AG,再判断△EPH≌△FQH,即可得出HE=HF;(4)应用推广:由前一个结论得到△AEF为正三角形,再依次判断△MHN∽△HFN∽△MEH,即可得出结论.
AG,再判断△EPH≌△FQH,即可得出HE=HF;(4)应用推广:由前一个结论得到△AEF为正三角形,再依次判断△MHN∽△HFN∽△MEH,即可得出结论.
试题解析:(1)特例发现,如图:
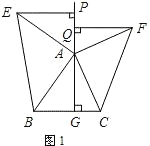 ∵∠PEA+∠PAE=90°,∠GAB+∠PAE=90°,∴∠PEA=∠GAB,∵∠EPA=∠AGB,AE=AB,∴△PEA≌△GAB,∴PE=AG,同理,△QFA≌△GAC,∴FQ=AG,∴PE=FQ;
∵∠PEA+∠PAE=90°,∠GAB+∠PAE=90°,∴∠PEA=∠GAB,∵∠EPA=∠AGB,AE=AB,∴△PEA≌△GAB,∴PE=AG,同理,△QFA≌△GAC,∴FQ=AG,∴PE=FQ;
(2)延伸拓展,如图:

∵∠PEA+∠PAE=90°,∠GAB+∠PAE=90°,∴∠PEA=∠GAB,∴∠EPA=∠AGB,∴△PEA∽△GAB,∴![]() ,∵AB=kAE,∴
,∵AB=kAE,∴![]() ,∴PE=
,∴PE=![]() AG,同理,△QFA∽△GAC,∴
AG,同理,△QFA∽△GAC,∴![]() ,∵AC=kAF,∴FQ=
,∵AC=kAF,∴FQ=![]() AG,∴PE=FQ,∵EP∥FQ,∴∠EPH=∠FQH,∵∠PHE=∠QHF,∴△EPH≌△FQH,∴HE=HF;
AG,∴PE=FQ,∵EP∥FQ,∴∠EPH=∠FQH,∵∠PHE=∠QHF,∴△EPH≌△FQH,∴HE=HF;
(3)深入探究,如图2,

在直线AG上取一点P,使得∠EPA═∠AGB,作FQ∥PE,∵∠EAP+∠BAG=180°﹣∠AGB,∠ABG+∠BAG=180°﹣∠AGB,∴∠EAP=∠ABG,∵∠EPA=∠AGB,∴△APE∽△BGA,∴![]() ,∵AB=kAE,∴PE=
,∵AB=kAE,∴PE=![]() AG,由于∠FQA=∠FAC=∠AGC=180°﹣∠AGB,同理可得,△AQF∽△CGA,∴
AG,由于∠FQA=∠FAC=∠AGC=180°﹣∠AGB,同理可得,△AQF∽△CGA,∴![]() ,∵AC=kAF,∴FQ=
,∵AC=kAF,∴FQ=![]() AG,∴EP=FQ,∵EP∥FQ,∴∠EPH=∠FQH,∵∠PHE=∠QHF,∴△EPH≌△FQH,∴HE=HF;
AG,∴EP=FQ,∵EP∥FQ,∴∠EPH=∠FQH,∵∠PHE=∠QHF,∴△EPH≌△FQH,∴HE=HF;
(4)应用推广,如图3,
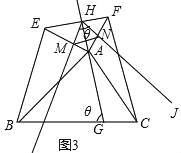
在前面条件及结论,得到,点H是EF中点,∴AE=AF,∵∠EAB=∠AGB,∠FAC=∠AGC∴∠EAB+∠FAC=180°∴∠EAF=360°﹣(∠EAB+∠FAC)﹣∠BAC=60°,∴△AEF为正三角形.又H为EF中点,∴∠EHM+∠IHJ=120°,∠IHJ+∠FHN=120°,∴∠EHM=∠FHN.∵∠AEF=∠AFE,∴△HEM∽△HFN,∴![]() ,∵EH=FH,∴
,∵EH=FH,∴![]() ,且∠MHN=∠HFN=60°,∴△MHN∽△HFN,∴△MHN∽△HFN∽△MEH,在△HMN中,∠MHN=60°,根据三角形中大边对大角,∴要MN最小,只有△HMN是等边三角形,∴∠AMN=60°,∵∠AEF=60°,MN∴MN∥EF,∵△AEF为等边三角形,∴MN为△AEF的中位线,∴MNmin=
,且∠MHN=∠HFN=60°,∴△MHN∽△HFN,∴△MHN∽△HFN∽△MEH,在△HMN中,∠MHN=60°,根据三角形中大边对大角,∴要MN最小,只有△HMN是等边三角形,∴∠AMN=60°,∵∠AEF=60°,MN∴MN∥EF,∵△AEF为等边三角形,∴MN为△AEF的中位线,∴MNmin=![]() EF=
EF=![]() ×2=1.
×2=1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市为打造“绿色城市”,积极投入资金进行园林绿化工程.2016年投资2 000万元,之后投资逐年增加,预计2018年投资2 420万元.求这两年投资的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图形似“w”的函数是由抛物线y1的一部分,其表达式为:y1=![]() (x2﹣2x﹣3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.
(x2﹣2x﹣3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.
(1)求A,B,C三点的坐标和曲线y2的表达式;
(2)我们把其中一条对角线被另一条对角线垂直且平分的四边形称为筝形.过点C作x轴的平行线与曲线y1交于另一个点D,连接AD.试问:在曲线y2上是否存在一点M,使得四边形ACDM为筝形?若存在,计算出点M的横坐标,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式计算正确的是( )
A.2a2+3a2=5a4
B.(﹣2ab)3=﹣6ab3
C.(3a+b)(3a﹣b)=9a2﹣b2
D.a3(﹣2a)=﹣2a3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com