
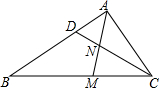
 如图,△ABC中,D是BA边上一点,AM是∠BAC的角平分线,交CD于N,AD=4,BD=5,AC=6,则AM:AN=2:3.
如图,△ABC中,D是BA边上一点,AM是∠BAC的角平分线,交CD于N,AD=4,BD=5,AC=6,则AM:AN=2:3. 分析 过C作CQ∥AM交BA延长线于Q,过M作MP∥CD交AB于P,根据角平分线性质得出$\frac{AB}{AC}$=$\frac{BM}{CM}$=$\frac{9}{6}$,根据平行线得出$\frac{BM}{CM}$=$\frac{BP}{DP}$=$\frac{3}{2}$,求出PD长,即可得出答案.
解答 解: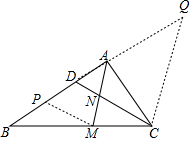
过C作CQ∥AM交BA延长线于Q,过M作MP∥CD交AB于P,
∵CQ∥AM,
∴∠Q=∠BAM,∠CAM=∠ACQ,
∵AM平分∠BAC,
∴∠BAM=∠CAM,
∴∠Q=∠ACQ,
∵AC=AQ,
∵AM∥CQ,
∴$\frac{AB}{AQ}$=$\frac{BM}{CM}$,
∴$\frac{AB}{AC}$=$\frac{BM}{CM}$,
∵AD=4,BD=5,AB=4+5=9,AC=6,
∴$\frac{BM}{CM}$=$\frac{9}{6}$=$\frac{3}{2}$,
∵MP∥CD,
∴$\frac{BP}{PD}$=$\frac{BM}{CM}$=$\frac{3}{2}$,
∵BD=5,
∴BP=3,PD=2,
∵CD∥PM,
∴△ADN∽△APM,
∴$\frac{AN}{AM}$=$\frac{AD}{AP}$=$\frac{4}{4+2}$=$\frac{2}{3}$,
故答案为:2:3.
点评 本题考查了平行线分线段成比例定理和相似三角形的性质和判定,能正确作出辅助线和得出比例式是解此题的关键.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 作物名称 | 蔬菜 | 果树 | 药材 |
| 每亩地所需的人数(人) | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
| 每亩地的预测利润(元) | 11000 | 7500 | 6000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
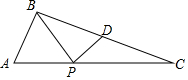 如图,△ABC中,AB=$\sqrt{5}$,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为2或5-$\sqrt{5}$.
如图,△ABC中,AB=$\sqrt{5}$,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为2或5-$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com