
【题目】已知抛物线![]() 与x轴交于两点A、
与x轴交于两点A、![]() 点A在x轴的正半轴上,点B在x轴的负半轴上
点A在x轴的正半轴上,点B在x轴的负半轴上![]() 与y轴交于点C.
与y轴交于点C.
![]() 求m的取值范围;
求m的取值范围;
![]() 如果
如果![]() :
:![]() :1,在该抛物线对称轴右边图象上求一点P的坐标,使得
:1,在该抛物线对称轴右边图象上求一点P的坐标,使得![]() .
.
【答案】(1)m>-3;(2)![]() 点坐标为
点坐标为![]() .
.
【解析】试题分析:
(1)由题意可得△=![]() ,说明抛物线与x轴总有两个不同的交点,由此根据抛物线与x轴的两个交点位于原点左、右两侧可得:-(m+3)<0,由此即可解得m的取值范围;
,说明抛物线与x轴总有两个不同的交点,由此根据抛物线与x轴的两个交点位于原点左、右两侧可得:-(m+3)<0,由此即可解得m的取值范围;
(2)设线段OB=k,则线段OA=3k,由题意可得点A的坐标为(3k,0),点B的坐标为(-k,0),则3k和-k是一元二次方程![]() 的两根,由一元二次方程根与系数的关系列出方程组,解方程组即可求得k和m的值,从而可得点B的坐标和抛物线的解析式,设PC和x轴的交点为D,由∠PCO=∠BCO,可得点D和点B关于原点对称,由此可得点D的坐标,从而可的直线PC的解析式,由PC的解析式和抛物线的解析式组成方程组,解方程组即可求得点P的坐标.
的两根,由一元二次方程根与系数的关系列出方程组,解方程组即可求得k和m的值,从而可得点B的坐标和抛物线的解析式,设PC和x轴的交点为D,由∠PCO=∠BCO,可得点D和点B关于原点对称,由此可得点D的坐标,从而可的直线PC的解析式,由PC的解析式和抛物线的解析式组成方程组,解方程组即可求得点P的坐标.
试题解析:
(1)∵抛物线![]() 中,
中,
△=![]() ,
,
∴该抛物线与x轴总有两个不同的交点,
又∵该抛物线与x轴的两个交点一个在原点左边,一个在原点右边,
∴-(m+3)<0,解得:m>-3;
(2)设![]() ,则由题意可得
,则由题意可得![]() ,点A、B的坐标分别为:(3k,0)、(-k,0),
,点A、B的坐标分别为:(3k,0)、(-k,0),
∴-k和3k是一元二次方程![]() 的两根,
的两根,
∴![]() ,解得:
,解得: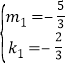 (不合题意,舍去),
(不合题意,舍去),![]() ,
,
∴抛物线的解析式为:![]() ,点B的坐标为(-1,0),点C的坐标为(0,3),
,点B的坐标为(-1,0),点C的坐标为(0,3),
如图,设点B关于原点的对称点是点D,则点D的坐标为(1,0),连接CD并延长交抛物线于点P,则此时∠PCO=∠BCO,
由点C的坐标为(0,3)、点D的坐标为(1,0)可得直线CD的解析式为:![]() ,
,
由![]() ,解得
,解得![]() ,
,![]() ,
,
∵点P不能与点C重合,
∴点P的坐标为(5,-12).


科目:初中数学 来源: 题型:
【题目】探究题
已知:如图1,![]() ,
,![]() .求证:
.求证:![]() .
.

老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线![]() ,然后在平行线间画了一点
,然后在平行线间画了一点![]() ,连接
,连接![]() 后,用鼠标拖动点
后,用鼠标拖动点![]() ,分别得到了图2,3,4,小颖发现图3正是上面题目的原型,于是她由上题的结论猜想到图2和4中的
,分别得到了图2,3,4,小颖发现图3正是上面题目的原型,于是她由上题的结论猜想到图2和4中的![]() 、
、![]() 与
与![]() 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小颖操作探究的基础上,继续完成下面的问题:
①猜想图2中![]() 、
、![]() 与
与![]() 之间的数量关系并加以证明;
之间的数量关系并加以证明;
②补全图4,直接写出![]() 、
、![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,![]() 轴于点C,交的图象于点
轴于点C,交的图象于点![]() 轴于点D,交的图象于点B,当点P在的图象上运动时,下列结论错误的是( )
轴于点D,交的图象于点B,当点P在的图象上运动时,下列结论错误的是( )

A. ![]() 与
与![]() 的面积相等
的面积相等
B. 当点A是PC的中点时,点B一定是PD的中点
C. 只有当四边形OCPD为正方形时,四边形PAOB的面积最大
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了提高绿化品位,美化环境,准备将一块周长为114 m的长方形草地,设计成长和宽分别相等的9块长方形(如图所示),种上各种花卉,经市场预测,每平方米绿化费为100元.
(1)求出每个小长方形的长和宽;
(2)请计算出完成这块草地的绿化工程预计投入资金多少元.

查看答案和解析>>
科目:初中数学 来源: 题型:
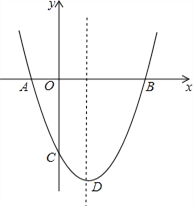
【题目】如图,抛物线![]() 与y轴交于点
与y轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点D为抛物线的顶点.
,点D为抛物线的顶点.
![]() 求抛物线解析式和顶点D的坐标;
求抛物线解析式和顶点D的坐标;
![]() 求抛物线与x轴的两交点A、B的坐标;
求抛物线与x轴的两交点A、B的坐标;
![]() 你可以直接写出不等式
你可以直接写出不等式![]() 的解集吗?
的解集吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,王亮同学从家里跑步到体育馆,在那里锻炼了一阵后又走到某书店去买书, 然后散步走回家如图反映的是在这一过程中,王亮同学离家的距离 s(千米)与离家的时间 t(分钟)之间的关系,请根据图象解答下列问题:
(1)体育馆离家的距离为 千米,书店离家的距离为_____千米;王亮同学在书店待了______分钟.
(2)分别求王亮同学从体育馆走到书店的平均速度和从书店出来散步回家的平均速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字:
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由如图给出了若干个边长为![]() 和边长为
和边长为![]() 的小正方形纸片及若干个边长为
的小正方形纸片及若干个边长为![]() 的长方形纸片,如图是由如图提供的几何图形拼接而得,可以得到
的长方形纸片,如图是由如图提供的几何图形拼接而得,可以得到![]()
![]()
请解答下列问题:
(1)请写出如图中所表示的数学等式:______________________________;
(2)用(1)中所得到的结论,解决下面的问题:已知![]() 则
则![]() 的值为_________.
的值为_________.
(3)①请按要求利用所给的纸片拼出一个长方形,要求所拼出图形的面积为![]() 并将所拼出的图像画在的方框中;
并将所拼出的图像画在的方框中;
②再利用另一种计算面积的方法,可将多项式![]() 分解因式,即
分解因式,即![]() _________.
_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块长为a(cm),宽为b(cm)(a>b)的矩形黑板的四周,镶上宽为x(cm)的木板,得到一个新的矩形.
(1)试用含a,b,x的代数式表示新矩形的长和宽;
(2)试判断原矩形的长、宽与新矩形的长、宽是不是比例线段,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com