
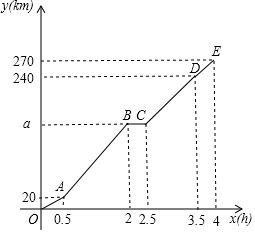
 小胜一家自驾去离家(点O)270km处的某景区(点E)旅游,如图折线OABCDE表示他们离家的路程y(km)与出发的时间x(h)之间的函数图象,其中AB段的行驶速度为90km/h,BC段表示小胜一家在高速服务区下车休息.
小胜一家自驾去离家(点O)270km处的某景区(点E)旅游,如图折线OABCDE表示他们离家的路程y(km)与出发的时间x(h)之间的函数图象,其中AB段的行驶速度为90km/h,BC段表示小胜一家在高速服务区下车休息.分析 (1)根据函数图象可以直接写出从家到景区一共花了多少时间;
(2)根据函数图象中的数据和AB段的行驶速度为90km/h,可以求得a的值;
(3)根据a的值和函数图象中的数据可以求得当2.5≤x≤3.5时,y关于x的函数表达式.
解答 解:(1)由图象可得,
从家到景区一共花了4h;
(2)由题意可得,
a=20+90×(2-0.5)=20+90×1.5=20+135=155,
即a的值是155;
(3)当2.5≤x≤3.5时,y关于x的函数表达式是y=kx+b,
$\left\{\begin{array}{l}{2.5k+b=155}\\{3.5k+b=240}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=85}\\{b=-57.5}\end{array}\right.$,
即当2.5≤x≤3.5时,y关于x的函数表达式是y=85x-57.5.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,求出相应的函数解析式,利用数形结合的思想解答.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
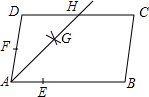 如图,在?ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
如图,在?ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )| A. | DH=BC | B. | CH=DH | C. | AG平分∠DAB | D. | AD=DH |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
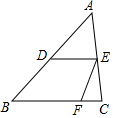 如图,在△ABC中,D、E分别是AB、AC的中点,点F在BC上,DE是∠AEF的角平分线,若∠C=80°,则∠EFB的度数是( )
如图,在△ABC中,D、E分别是AB、AC的中点,点F在BC上,DE是∠AEF的角平分线,若∠C=80°,则∠EFB的度数是( )| A. | 100° | B. | 110° | C. | 115° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
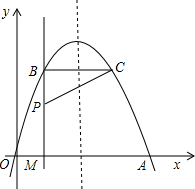 如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.
如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com