
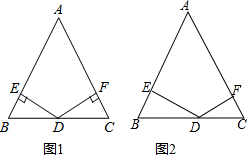
 (1)如图1,等腰三角形ABC中,AB=AC,点D是BC的中点,DE⊥AB于点E、DF⊥AC于点F.求证:DE=DF;
(1)如图1,等腰三角形ABC中,AB=AC,点D是BC的中点,DE⊥AB于点E、DF⊥AC于点F.求证:DE=DF;分析 (1)连接AD,D是BC的中点,那么AD就是等腰三角形ABC底边上的中线,根据等腰三角形三线合一的特性,可知道AD也是∠BAC的角平分线,根据角平分线的点到角两边的距离相等,那么DE=DF;
(2)连接AD,根据三角形的面积公式即可得到$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=12,进而求得DE+DF的值.
解答  (1)证明:如图1,连接AD.
(1)证明:如图1,连接AD.
∵AB=AC,点D是BC边上的中点,
∴AD平分∠BAC,
∵DE、DF分别垂直AB、AC于点E和F.
∴DE=DF.
(2)解:不变.
如图2所示:连接AD,
∵AB=AC=13,BC=10,
∴△ABC底边BC上的高=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∴△ABC的面积=$\frac{1}{2}$×BC×12=60,
∴$\frac{1}{2}$AB•DE+$\frac{1}{2}$AC•DF=60,
∴DE+DF=$\frac{120}{13}$,
故答案为:$\frac{120}{13}$.
点评 本题考查的是勾股定理及等腰三角形的性质,熟知等腰三角形三线合一的性质是解答此题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
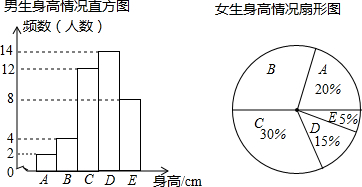 为了解我校初一年级学生的身高情况,随机对初一男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据调查所得数据绘制如图所示的统计图表.由图表中提供的信息,回答下列问题:
为了解我校初一年级学生的身高情况,随机对初一男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据调查所得数据绘制如图所示的统计图表.由图表中提供的信息,回答下列问题:| 组别 | 身高(cm) |
| A | x<150 |
| B | 150≤x<155 |
| C | 155≤x<160 |
| D | 160≤x<165 |
| E | x≥165 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com