Question

在Rt△ABC中，∠C=90°，斜边c=5，两直角边的长a，b是关于x的一元二次方程x²-mx+2m-2=0的两个根，求Rt△ABC中较小锐角的正弦值．

Answer 1

【答案】分析：根据一元二次方程的根与系数的关系求得m的值后，再求得方程的解，求出较小锐角的正弦值．
解答：解：∵a，b是方程x²-mx+2m-2=0的解，
∴a+b=m，ab=2m-2，
在Rt△ABC中，由勾股定理得，a²+b²=c²，
而a²+b²=（a+b）²-2ab，c=5，
∴a²+b²=（a+b）²-2ab=25，
即：m²-2（2m-2）=25
解得，m₁=7，m₂=-3，
∵a，b是Rt△ABC的两条直角边的长．
∴a+b=m＞0，m=-3不合题意，舍去．
∴m=7，
当m=7时，原方程为x²-7x+12=0，
解得，x₁=3，x₂=4，
不妨设a=3，则sinA==，
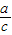
∴Rt△ABC中较小锐角的正弦值为．
点评：本题难度较大，利用了一元二次方程的根与系数的关系，勾股定理，正弦的概念求解．
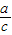