
【题目】已知点A,B在数轴上对应的实数分别是a,b,其中a,b满足|a﹣2|+(b+1)2=0.
(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程x﹣1=![]() x+1的解,在数轴上是否存在点P,使PA+PB=PC,若存在,求出点P对应的数;若不存在,说明理由;
x+1的解,在数轴上是否存在点P,使PA+PB=PC,若存在,求出点P对应的数;若不存在,说明理由;
(3)在(1)和(2)的条件下,点A,B,C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动,点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,设运动时间为t秒,试探究:随着时间t的变化,AB与BC满足怎样的数量关系?请写出相应的等式.
【答案】(1)3;(2)﹣2或0;(3)t≤![]() 时,AB+BC=7;当t>
时,AB+BC=7;当t>![]() 时,BC﹣AB=7.
时,BC﹣AB=7.
【解析】
(1)根据绝对值及完全平方的非负性,可得出a、b的值,继而可得出线段AB的长;
(2)先求出x的值,再由PA+PB=PC,可得出点P对应的数;
(3)根据A,B,C的运动情况确定AB,BC的变化情况,再根据t的取值范围即可求出AB与BC满足的数量关系.
(1)∵|a﹣2|+(b+1)2=0,∴a=2,b=﹣1,∴线段AB的长为:2﹣(﹣1)=3;
(2)解方程x﹣1=![]() x+1,得x=3,则点C在数轴上对应的数为3.
x+1,得x=3,则点C在数轴上对应的数为3.
![]()
由图知,满足PA+PB=PC时,点P不可能在C点右侧,不可能在线段AC上,①如果点P在点B左侧时,2﹣x+(﹣1)﹣x=3﹣x,解得:x=﹣2;
③当P在A、B之间时,3﹣x=3,解得:x=0.
故所求点P对应的数为﹣2或0;
(3)t秒钟后,A点位置为:2﹣t,B点的位置为:﹣1+4t,C点的位置为:3+9t,BC=3+9t﹣(﹣1+4t)=4+5t,AB=|﹣1+4t﹣2+t|=|5t﹣3|,分两种情况讨论:
①当t≤![]() 时,AB+BC=3﹣5t+4+5t=7;
时,AB+BC=3﹣5t+4+5t=7;
②当t>![]() 时,BC﹣AB=4+5t﹣(5t﹣3)=7.
时,BC﹣AB=4+5t﹣(5t﹣3)=7.
综上所述:当t≤![]() 时,AB+BC=7;当t>
时,AB+BC=7;当t>![]() 时,BC﹣AB=7.
时,BC﹣AB=7.


科目:初中数学 来源: 题型:
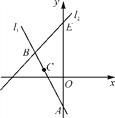
【题目】如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.
(1)求点C的坐标和直线l1的解析式;
(2)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
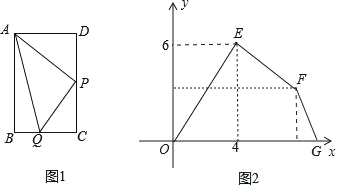
【题目】如图1,在长方形ABCD中,点P是CD中点,点Q从点A开始,沿着A→B→C→P的路线匀速运动,设△APQ的面积是y,点Q经过的路线长度为x,图2坐标系中折线OEFG表示y与x之间的函数关系,点E的坐标为(4,6),则点G的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示. 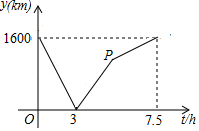
(1)填空:动车甲的速度为(km/h),动车乙的速度为(km/h);
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)两车何时相距1200km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2014年12月28日北京公交地铁调价以来,人们的出行成本发生了较大的变化. 小林根据新闻,将地铁和公交车的票价绘制成了如下两个表格。(说明:表格中“6~12公里”指的是大于6公里,小于等于12公里,其他类似)
|
| ||||||||||||||||||||||||||||||
根据以上信息回答下列问题:
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣。
(1)如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费________元;
(2)如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交________元;
(3)小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里。已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元。请问小林乘坐地铁和公交车的里程分别是多少公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
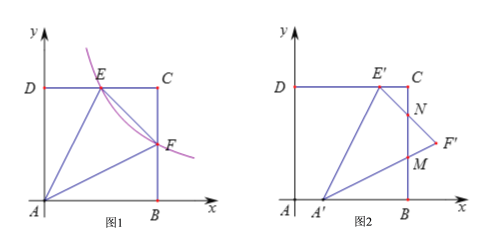
【题目】如图1,正方形ABCD的边长为4,以AB所在的直线为x轴,以AD所在的直线为y轴建立平面直角坐标系![]() 反比例函数
反比例函数![]() 的图象与CD交于E点,与CB交于F点.
的图象与CD交于E点,与CB交于F点.
(1)求证:![]() ;
;
(2)若![]() 的面积为6,求反比例函数的解析式;
的面积为6,求反比例函数的解析式;
(3)在(2)的条件下,将![]() 沿x轴的正方向平移1个单位后得到
沿x轴的正方向平移1个单位后得到![]() ,如图2,线段
,如图2,线段![]() 与
与![]() 相交于点M,线段
相交于点M,线段![]() 与BC相交于点N.求
与BC相交于点N.求![]() 与正方形ABCD的重叠部分面积.
与正方形ABCD的重叠部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD,直线EF与AB,CD分别相交于点E,F.
(1)如图1,若∠1=60°,求∠2,∠3的度数.

(2)若点P是平面内的一个动点,连结PE,PF,探索∠EPF,∠PEB,∠PFD三个角之间的关系.
①当点P在图(2)的位置时,可得∠EPF=∠PEB+∠PFD请阅读下面的解答过程并填空(理由或数学式)
解:如图2,过点P作MN∥AB
则∠EPM=∠PEB(_______)
∵AB∥CD(已知)MN∥AB(作图)
∴MN∥CD(_______)
∴∠MPF=∠PFD (_______)
∴_____=∠PEB+∠PFD(等式的性质)
即:∠EPF=∠PEB+∠PFD
②拓展应用,当点P在图3的位置时,此时∠EPF=80°,∠PEB=156°,则∠PFD=_____度.
③当点P在图4的位置时,请直接写出∠EPF,∠PEB,∠PFD三个角之间关系_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com