
分析 (1)先根据互为相反数的两个数的和为0,得$\sqrt{8-2(x+3)}$+(2y-4)2=0,再根据非负数的意义,列方程组求出x、y的值;然后由等腰三角形的性质求出其周长;
(2)先将x=1,y=2代入所求代数式,再根据$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$)把每一个分数写成两个分数的差,然后化简即可.
解答 解:(1)依题意,得$\sqrt{8-2(x+3)}$+(2y-4)2=0,
∴$\left\{\begin{array}{l}{8-2(x+3)=0}\\{2y-4=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
当腰长为1时,不满足三角形三边关系定理,故腰长为2,此时,周长=2+2+1=5;
(2)∵x=1,y=2,
∴原式=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{49×51}$
=$\frac{1}{2}$[(1-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{5}$)+($\frac{1}{5}$-$\frac{1}{7}$)+…+($\frac{1}{49}$-$\frac{1}{51}$)
=$\frac{1}{2}$×(1-$\frac{1}{51}$)
=$\frac{25}{51}$.
点评 本题考查了相反数的定义,非负数的性质,二元一次方程组的解法,等腰三角形的性质,三角形三边关系定理及有理数的运算,涉及的知识点较多,难度中等.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:解答题
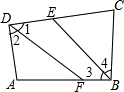 如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F.
如图,在四边形ABCD中,∠ABC、∠ADC的平分线分别与CD、AB相交于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x-3=0}\\{3x-2y=7}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x-y=3}\\{3xy=8}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=3}\\{x-z=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{2}x+\frac{3}{y}=4}\\{\frac{1}{3}x+\frac{1}{2}y=1}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com