
【题目】我们把对角线互相垂直的四边形叫做垂美四边形.
(1)(概念理解)在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的是___________.
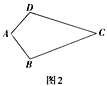
(2)(性质探究)如图2,试探索垂美四边形ABCD的两组对边AB,CD与BC ,AD之间的数量关系,写出证明过程。
(3)(问题解决)如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外做正方形ACFG和正方形ABDE,连接CE,BG,GE, 已知AC=![]() ,BC=1 求GE的长.
,BC=1 求GE的长.

【答案】菱形、正方形
【解析】(1)根据垂美四边形的定义进行判断即可;
(2)根据垂直的定义和勾股定理解答即可;
(3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算.
(1)菱形的对角线互相垂直,符合垂美四边形的定义,
正方形的对角线互相垂直,符合垂美四边形的定义,
而平行四边形、矩形的对角线不一定垂直,不符合垂美四边形的定义,
故答案为:菱形、正方形;
(2)猜想结论:AD2+BC2=AB2+CD2,证明如下:
如图2,连接AC、BD,交点为E,则有AC⊥BD,
∵AC⊥BD,
∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,
AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2;
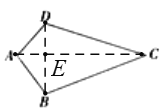
(3)连接CG、BE,设AB与CE的交点为M
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
又∵AG=AC,AB=AE,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,
又∠AEC+∠AME=90°,∠AME=∠BMC,
∴∠ABG+∠BMC=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,
∵AC=![]() ,BC=1 ∴AB=2,
,BC=1 ∴AB=2,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
GE的长是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点. 
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,当PA+PB最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知|a+3|与(b+1)2互为相反数,a、b分别对应数轴上的点A、B.
(1)求a、b的值.
(2)数轴上原点右侧存在点C,设甲、乙、丙三个动点分别从A、B、C三点同时运动,甲、乙向数轴正方向运动,丙向数轴负方向运动,甲、乙、丙运动速度分别为1、![]() 、2(单位长度每秒),若它们在数轴上某处相遇,请求出C点对应的数是多少?
、2(单位长度每秒),若它们在数轴上某处相遇,请求出C点对应的数是多少?
(3)运用(2)中所求C点对应的数,若甲、乙、丙出发地及速度大小均不变,同时向数轴负方向运动,问丙先追上谁?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣1,0,1,2这5个数中,随机抽取一个数记为a,则使关于x的不等式组 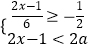 有解,且使关于x的一元一次方程
有解,且使关于x的一元一次方程 ![]() +1=
+1= ![]() 的解为负数的概率为 .
的解为负数的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
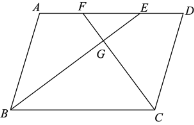
【题目】如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,写出求BE的长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为3.6米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.6米,看台最低点A与旗杆底端D之间的距离为16米(C,A,D在同一条直线上).
(1)求看台最低点A到最高点B的坡面距离;
(2)一面红旗挂在旗杆上,固定红旗的上下两个挂钩G、H之间的距离为1.2米,下端挂钩H与地面的距离为1米,要求用30秒的时间将红旗升到旗杆的顶端,求红旗升起的平均速度(计算结果保留两位小数)(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于与坐标轴不平行的直线l和点P,给出如下定义:过点P作x轴,y轴的垂线,分别交直线l于点M,N,若PM+PN≤4,则称P为直线l的近距点,特别地,直线上l所有的点都是直线l的近距点.已知点A(-![]() ,0),B(0,2),C(-2,2).
,0),B(0,2),C(-2,2).
(1)当直线l的表达式为y=x时,
①在点A,B,C中,直线l的近距点是 ;
②若以OA为边的矩形OAEF上所有的点都是直线l的近距点,求点E的纵坐标n的取值范围;
(2)当直线l的表达式为y=kx时,若点C是直线l的近距点,直接写出k的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-16-(-1+![]() )÷3×[2-(-4)2]
)÷3×[2-(-4)2]
(2)解方程:![]() -
-![]() =-1
=-1
(3)先化简,再求值:2(x2-2xy)+[2y2-3(x2-2xy+y2)+x2],其中x=1,y=-![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com