

分析 发现:如图1中,作EH⊥CD于H.分别求出DH、CH即可.接CO交半圆于M、连接AC.则点C到半圆O上的点的最小距离为CM=OC-OM=$\sqrt{5}$-1,点C到半圆O上的点的最大距离为AC=2$\sqrt{2}$;
思考:(1)如图2中,当点B与点C重合时,半圆O与△CDE重叠部分的面积=S扇形OMC-S△OMC.
(2)如图3中,当点A在线段CE上时,设BC=a,求出此时的x.如图4中,当点A在线段DE上时,求出此时x即可.
探究:求出⊙O与CE、DE相切时的x的值,结合(2)中结果,即可解决问题.
解答 解:发现:如图1中,作EH⊥CD于H.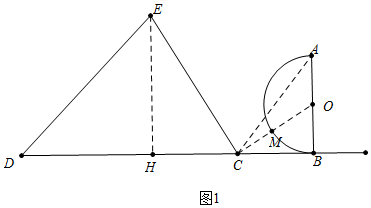
在Rt△DEH中,∵DE=3$\sqrt{2}$,∠D=45°,
∴∠D=∠DEH=45°,
∴EH=DH=3,
∵∠E=75°,
∴∠CEH=30°,
∴CH=$\sqrt{3}$,EC=2$\sqrt{3}$,
∴CD=3+$\sqrt{3}$.
连接CO交半圆于M、连接AC.则点C到半圆O上的点的最小距离为CM=OC-OM=$\sqrt{5}$-1,点C到半圆O上的点的最大距离为AC=2$\sqrt{2}$.
故答案为3+$\sqrt{3}$,$\sqrt{5}$-1,2$\sqrt{2}$.
思考:(1)如图2中,当点B与点C重合时,半圆O与△CDE重叠部分的面积=S扇形OMC-S△OMC.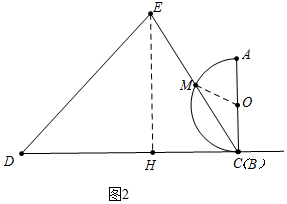
∵AC∥EH,
∴∠ACM=∠CEH=30°,
∵OM=OC,
∴∠OMC=∠OCM=30°,
∴∠COM=120°,
∴半圆O与△CDE重叠部分的面积=S扇形OMC-S△OMC=$\frac{120•π•{1}^{2}}{360}$-$\frac{1}{2}$$•\sqrt{3}$$•\frac{1}{2}$=$\frac{π}{3}$-$\frac{\sqrt{3}}{4}$.
(2)如图3中,当点A在线段CE上时,设BC=a
∵AB∥EH,
∴$\frac{AB}{EH}$=$\frac{BC}{CH}$,
∴$\frac{2}{3}$=$\frac{a}{\sqrt{3}}$
∴a=$\frac{2\sqrt{3}}{3}$.此时x=2+$\frac{2\sqrt{3}}{3}$
如图4中,当点A在线段DE上时,易知AB=BD=2,BH=1,此时x=3+$\sqrt{3}$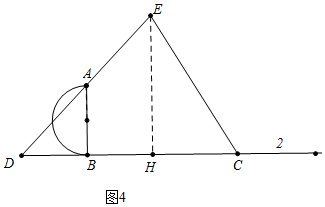
∴当直径AB完全落在△CDE内部(含端点在边界)时,x的取值范围是2+$\frac{2\sqrt{3}}{3}$≤x≤3+$\sqrt{3}$.
探究:当⊙O与DE相切时,设切点为N,连接ON、OD,在DB上取一点M,使得DM=OM.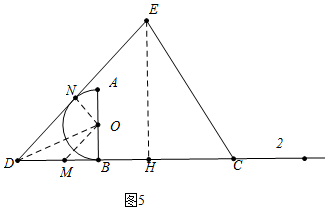
则易知∠ODN=∠ODM=22.5°,∠OMB=45°,
∴OM=DM=$\sqrt{2}$,BM=1,
∴BC=3+$\sqrt{3}$-($\sqrt{2}$+1)=2+$\sqrt{3}$-$\sqrt{2}$,
此时x=4+$\sqrt{3}$-$\sqrt{2}$,
如图6中,当⊙O与CE相切于点N时,易知∠OCB=∠OCN=60°,BC=$\frac{\sqrt{3}}{3}$,此时x=2-$\frac{\sqrt{3}}{3}$.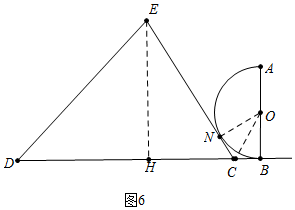
综上所述,当弧$\widehat{AB}$与△CDE的边有两个交点时2-$\frac{\sqrt{3}}{3}$<x≤2+$\frac{2\sqrt{3}}{3}$或x=4+$\sqrt{3}$-$\sqrt{2}$或3+$\sqrt{3}$<x<5+$\sqrt{3}$.
点评 本题考查圆综合题、等腰直角三角形的性质.30度的直角三角形的性质、切线的判定和性质、勾股定理平行线分线段成比例定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
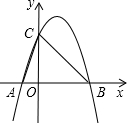 如图,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
如图,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
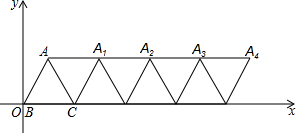 如图,在平面直角坐标系内,边长为4的等边△ABC的顶点B与原点重合,将△ABC绕顶点C顺时针旋转60°的△ACA1,将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,则A2017的坐标为(8070,2$\sqrt{3}$).
如图,在平面直角坐标系内,边长为4的等边△ABC的顶点B与原点重合,将△ABC绕顶点C顺时针旋转60°的△ACA1,将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,则A2017的坐标为(8070,2$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -2 | B. | -3 | C. | -4 | D. | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com