
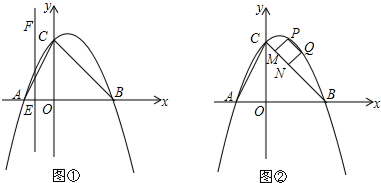
���� ��1�����ô���ϵ����������κ�������ʽ��
��2�����ݽ���ʽ���A�����꣬��ֱ��������AOC�ڿ������tan��CAO��ֵ��
��3�����ݵ�E���˶����ɷ������۵ó�S��t�ĺ�����ϵʽ��
��4����֤��MQ��OB���ɵó�ֱ��BC����ʽΪy=-x+4���ٸ��������ε����ʵó�MQ=PN�����M���꼴�ɣ�
��� �⣺��1����������y=ax2+x+c����B��4��0����C��0��4����
��$\left\{\begin{array}{l}{16a+4+c=0}\\{c=4}\end{array}\right.$���$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=4}\end{array}\right.$��
�������ߵı���ʽΪ$y=-\frac{1}{2}{x}^{2}+x+4$��
��2����y=0����-$\frac{1}{2}$x2+x+4=0��ã�x1=-2��x2=4��
��A��-2��0������OA=2��OC=4��
��tan��CAO=$\frac{OC}{OA}=\frac{4}{2}$=2��
��3����0��t��2ʱ����EF��AC��D��
��EF��y�ᣬ
���ADE�ס�ACO��
��$\frac{AE}{DE}=\frac{AO}{OC}$��$\frac{t}{DE}=\frac{2}{4}$��
��DE=2t��
��S=$\frac{1}{2}$AE•DE=$\frac{1}{2}$•t•2t=t2
��S=t2��0��t��2����
��2��t��6ʱ����EF��BC��G��
��EF��y�ᣬ
���BGE�ס�BCO��
��$\frac{EG}{EB}=\frac{OC}{OB}$��$\frac{EG}{6-t}=\frac{4}{4}$��
��FG=6-4��
��S=S��ABC-S��BGF��
=$\frac{1}{2}$��6��4-$\frac{1}{2}$•��6-t��•��6-t��
=$\frac{1}{2}$t2+6t-6��
��S=-$\frac{1}{2}$t2+6t-6��2��t��6����
����������S��t�ĺ�����ϵʽΪ��$S=\left\{\begin{array}{l}{{t}^{2}��0��t��2��}\\{-\frac{1}{2}{t}^{2}+6t-6��2��t��6��}\end{array}\right.$��
��4������MQ��PN���ڵ�I��
��OB=OC��
���OBC=��OCB=45�㣮
��������MNQP��
��PN��MQ����NMQ=45�㣮
���NMQ=��OBC��
��MQ��OB��
��PN��OB��
��ֱ��BC����ʽΪy=-x+4��
��Q��m��-$\frac{1}{2}{m}^{2}$+m+4����-x+4=-$\frac{1}{2}{m}^{2}$+m+4��
��x=$\frac{1}{2}{m}^{2}$-m��
��M��$\frac{1}{2}{m}^{2}$-m��-$\frac{1}{2}{m}^{2}$+m+4��
��I��$\frac{1}{4}{m}^{2}$��-$\frac{1}{2}{m}^{2}$+m+4����MQ=m-��$\frac{1}{2}{m}^{2}$-m��=2m-$\frac{1}{2}{m}^{2}$��
��${y}_{N}=-\frac{1}{4}{m}^{2}$+4��${y}_{N}=-\frac{1}{4}{m}^{2}+4$��${y}_{P}=-\frac{1}{2}��\frac{1}{4}{m}^{2}��^{2}+\frac{1}{4}{m}^{2}+4=-\frac{1}{32}{m}^{4}+\frac{1}{4}{m}^{2}+4$��
��$PN=-\frac{1}{32}{m}^{4}+\frac{1}{4}{m}^{2}+4-��-\frac{1}{4}{m}^{2}+4��=-\frac{1}{32}{m}^{4}+\frac{1}{2}{m}^{2}$��
��������MNQP��
��MQ=PN��
��2m-$\frac{1}{2}{m}^{2}$=-$\frac{1}{32}{m}^{4}+\frac{1}{2}{m}^{2}$��
��m��0��
��$2-\frac{1}{2}m=-\frac{1}{32}{m}^{3}+\frac{1}{2}m$
�����ã�64-16m=-m3+16m
16��4-m��=m��4+m����4-m����
��4-m��0��
��m��4+m��=16��
��m2+4m-16=0��
���m1=-2-$2\sqrt{5}$����ȥ��m2=-2+$2\sqrt{5}$��
��$\frac{1}{2}{m}^{2}$-m=14-$6\sqrt{5}$��-$\frac{1}{2}{m}^{2}$+m+4=$6\sqrt{5}$-10��
M��14-$6\sqrt{5}$��$6\sqrt{5}$-10����
���� ���⿼����Ƕ��κ�������ۺ�Ӧ�ã�����ϵ��������κ�������ʽ�dz��������ͣ���������Ľ���ؼ����ҳ�������˶����ɣ�����������Ӧ������ʾ�������������ν�ϡ��������ۼ�����˼���ǽ���Ĺؼ���


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �躯��y1=��x-k��2+k��y2=��x+k��2-k��ͼ���ཻ�ڵ�A������y1��y2��ͼ��Ķ���ֱ�ΪB��C��
�躯��y1=��x-k��2+k��y2=��x+k��2-k��ͼ���ཻ�ڵ�A������y1��y2��ͼ��Ķ���ֱ�ΪB��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
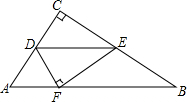 ��ͼ����ABC�У���C=90�㣬AC=6��BC=8��D��E�ֱ���AC��BC����DE��AB������ABC��DE�۵���ʹC������б��AB�ϵ�F������AF�ij��ǣ�������
��ͼ����ABC�У���C=90�㣬AC=6��BC=8��D��E�ֱ���AC��BC����DE��AB������ABC��DE�۵���ʹC������б��AB�ϵ�F������AF�ij��ǣ�������| A�� | 3.6 | B�� | 4 | C�� | 4.8 | D�� | 6.4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
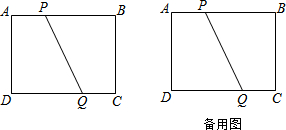
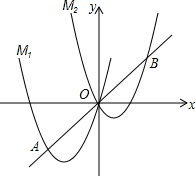 ��ͼ����������M1��y=ax2+4x����ƽ��3����λ��������ƽ��3����λ���õ�������M2��ֱ��y=x��M1��һ�������ΪA����M2��һ�������ΪB����A�ĺ�������-3��
��ͼ����������M1��y=ax2+4x����ƽ��3����λ��������ƽ��3����λ���õ�������M2��ֱ��y=x��M1��һ�������ΪA����M2��һ�������ΪB����A�ĺ�������-3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 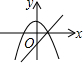 | B�� | 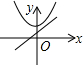 | C�� | 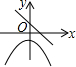 | D�� | 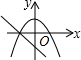 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com