
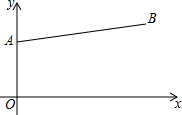
 已知:如图,点A(0,6),点B(14,8),在第四象限找点C,使得△ABC为等腰三角形,且∠C=45°,则点C的坐标为(2,-8)、(8+$\sqrt{2}$,-7$\sqrt{2}$)、(16,-6).
已知:如图,点A(0,6),点B(14,8),在第四象限找点C,使得△ABC为等腰三角形,且∠C=45°,则点C的坐标为(2,-8)、(8+$\sqrt{2}$,-7$\sqrt{2}$)、(16,-6). 分析 首先根据题意,判断出ABC为等腰三角形的三种情况:(1)两个腰是AB、AC;(2)两个腰是AC、BC;(3)两个腰是AB、BC;然后分类讨论,根据等腰三角形的两个腰的长度相等,以及两条相互垂直的直线的斜率的乘积是-1,分别求出点C的坐标各是多少即可.
解答 解:(1)如图1,当等腰三角形ABC的两个腰是AB、AC时,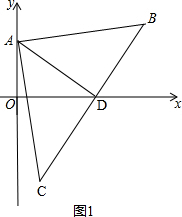 ,
,
设点C的坐标为(a,b),BC的中点D的坐标为($\frac{a+14}{2},\frac{b+8}{2}$),
因为∠C=45°,所以∠B=45°,
所以∠BAC=180-45-45=90°,
即△ABC为等腰直角三角形,
所以$\frac{8-6}{14-0}×\frac{b-6}{a-0}=-1$,
整理,可得b=6-7a…(1);
因为D是BC的中点,
所以AD⊥BC,
所以$\frac{\frac{b+8}{2}-6}{\frac{a+14}{2}-0}×\frac{b-8}{a-14}=-1$,
整理,可得a2+b2-12b-164=0…(2),
把(1)代入(2),解得a=2,
所以b=6-7×2=-8,
所以点C的坐标为(2,-8).
(2)如图2,当等腰三角形ABC的两个腰是AC、BC时, ,
,
设点C的坐标为(a,b),AB的中点E的坐标为($\frac{0+14}{2},\frac{6+8}{2}$),
即点E的坐标为(7,7),
因为E是AB的中点,
所以AB⊥CE,
所以$\frac{8-6}{14-0}×\frac{b-7}{a-7}=-1$,
整理,可得b=56-7a…(1),
因为∠C=45°,
所以$\frac{b-6}{a}$-$\frac{b-8}{a-14}$=1+$\frac{b-6}{a}$•$\frac{b-8}{a-14}$,
整理,可得a2+b2-16a-36=0…(2);
把(1)代入(2),解得a=8±$\sqrt{2}$,
根据图示,可得C点的横坐标大于E点的横坐标,
所以a=8+$\sqrt{2}$,
所以b=56-7×(8+$\sqrt{2}$)=-7$\sqrt{2}$,
所以点C的坐标为(8+$\sqrt{2}$,-7$\sqrt{2}$).
(3)如图3,当等腰三角形ABC的两个腰是AB、BC时, ,
,
设点C的坐标为(a,b),AC的中点F的坐标为($\frac{a+0}{2},\frac{b+6}{2}$),
因为∠C=45°,所以∠BAC=45°,
所以∠B=180-45-45=90°,
即△ABC为等腰直角三角形,
所以$\frac{8-6}{14-0}×\frac{b-8}{a-14}=-1$,
整理,可得b=106-7a…(1);
因为F是AC的中点,
所以BF⊥AC,
所以$\frac{\frac{b+6}{2}-8}{\frac{a+0}{2}-14}×\frac{b-6}{a-0}=-1$,
整理,可得a2+b2-28a-16b+60=0…(2),
把(1)代入(2),解得a=12或a=16,
根据图示,可得C点的横坐标大于B点的横坐标,
所以a=16,
所以b=106-7×16=-6,
所以点C的坐标为(16,-6).
综上,可得
点C的坐标为(2,-8)、(8+$\sqrt{2}$,-7$\sqrt{2}$)、(16,-6).
故答案为:(2,-8)、(8+$\sqrt{2}$,-7$\sqrt{2}$)、(16,-6).
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力;解答此题的关键是判断出△ABC为等腰三角形的三种情况:(1)两个腰是AB、AC;(2)两个腰是AC、BC;(3)两个腰是AB、BC.
(2)此题还考查了等腰三角形的性质,以及两条相互垂直的直线的特征,要熟练掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=15,b=8,c=17 | B. | a=12,b=14,c=15 | C. | a=$\sqrt{41}$,b=4,c=5 | D. | a=7,b=24,c=25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形的对角线上有一个小孔,经过小孔剪一刀(不剪曲线和折线)可以将剪下的两片拼成一个三角形,拼成的三角形内部没有小孔,如图1;图2中的正方形中也有一个小孔,但它不在对角线上,将它剪成三片,用剪成的三片拼成一个三角形,要求拼成的三角形内部没有小孔.仿照图1把剪切线和拼成的三角形画出来.
如图,正方形的对角线上有一个小孔,经过小孔剪一刀(不剪曲线和折线)可以将剪下的两片拼成一个三角形,拼成的三角形内部没有小孔,如图1;图2中的正方形中也有一个小孔,但它不在对角线上,将它剪成三片,用剪成的三片拼成一个三角形,要求拼成的三角形内部没有小孔.仿照图1把剪切线和拼成的三角形画出来.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com