
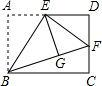
 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=$\sqrt{96}$,则DF的长为 ( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=$\sqrt{96}$,则DF的长为 ( )| A. | 2 | B. | 4 | C. | $\sqrt{6}$ | D. | $2\sqrt{3}$ |
分析 根据点E是AD的中点以及翻折的性质可以求出AE=DE=EG,然后利用“HL”证明△EDF和△EGF全等,根据全等三角形对应边相等可证得DF=GF;设FD=x,表示出FC、BF,然后在Rt△BCF中,利用勾股定理列式进行计算即可.
解答 解:∵E是AD的中点,
∴AE=DE,
∵△ABE沿BE折叠后得到△GBE,
∴AE=EG,AB=BG,
∴ED=EG,
∵在矩形ABCD中,
∴∠A=∠D=90°,
∴∠EGF=90°,
∵在Rt△EDF和Rt△EGF中,$\left\{\begin{array}{l}{ED=EG}\\{EF=EF}\end{array}\right.$,
∴Rt△EDF≌Rt△EGF(HL),
∴DF=FG,
设DF=x,则BF=6+x,CF=6-x,
在Rt△BCF中,($\sqrt{96}$)2+(6-x)2=(6+x)2,
解得x=4.
故选:B.
点评 此题是折叠问题,主要考查了矩形的性质,全等三角形的判定与性质,勾股定理的应用,翻折的性质,熟记性质,找出三角形全等的条件ED=EG是解题的关键.是一道典型的折叠问题.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
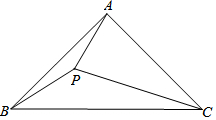 已知,如图,在△ABC中,AB=AC,∠BAC=α,且60°<α<120°,P是△ABC内部一点,且PC=AC,∠PCA=120°-α.
已知,如图,在△ABC中,AB=AC,∠BAC=α,且60°<α<120°,P是△ABC内部一点,且PC=AC,∠PCA=120°-α.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
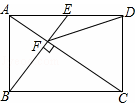 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有①②③⑤.
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有①②③⑤.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
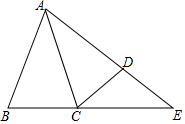 如图△ABC中,AB=AC=8,∠BAC=30°,现将△ABC绕点A逆时针旋转30°得到△ACD,延长AD、BC交于点E,则DE的长是4$\sqrt{3}$-4.
如图△ABC中,AB=AC=8,∠BAC=30°,现将△ABC绕点A逆时针旋转30°得到△ACD,延长AD、BC交于点E,则DE的长是4$\sqrt{3}$-4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交于点A(-2,0),
如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交于点A(-2,0),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
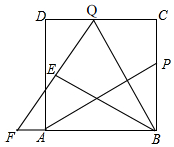 如图,P为边长为6的正方形ABCD的边BC上一动点(P与B、C不重合),Q在CD上,且CQ=BP,连接AP、BQ,将△BQC沿BQ所在的直线翻折得到△BQE,延长QE交BA的延长线于点F.
如图,P为边长为6的正方形ABCD的边BC上一动点(P与B、C不重合),Q在CD上,且CQ=BP,连接AP、BQ,将△BQC沿BQ所在的直线翻折得到△BQE,延长QE交BA的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com