
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
(1)求这条抛物线所对应的函数解析式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标;
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.


【解析】(1)根据题意,y=ax2+bx+c的对称轴为x=1,且过A(-1,0),C(0,-3),可得
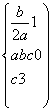 解得
解得![]()
∴抛物线所对应的函数解析式为y=x2-2x-3.
(2)由y=x2-2x-3可得,抛物线与x轴的另一交点B(3,0)如图①,连接BC,交对称轴x=1于点M.因为点M在对称轴上,MA=MB.所以直线BC与对称轴x=1的交点即为所求的M点.
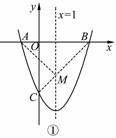

设直线BC的函数关系式为y=kx+b,由B(3,0),C(0,-3),解得y=x-3,由x=1,解得y=-2.
故当点M的坐标为(1,-2)时,点M到点A的距离与到点C的距离之和最小.
(3)如图②,设此时点P的坐标为(1,m),抛物线的对称轴交x轴于点F(1,0).连接PC、PB,作PD垂直y轴于点D,则D(0,m).
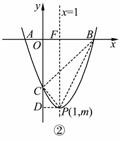

在Rt△CDP中,
CD=|m-(-3)|=|m+3|,DP=1,
∴CP2=CD2+DP2=(m+3)2+1.
在Rt△PFB中,PF=|m|,FB=3-1=2,
∴PB2=PF2+FB2=m2+4.
在Rt△COB中,CB2=OB2+OC2=32+32=18.
当∠PCB=90°时,有CP2+CB2=PB2.
即(m+3)2+1+18=m2+4.解得m=-4.
∴使∠PCB=90°的点P的坐标为(1,-4).


科目:初中数学 来源: 题型:
如图,已知抛物线y=x![]() -ax+a
-ax+a![]() -4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
-4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
(1)求a的值;
(2)当四边形ODPQ为矩形时,求这个矩形的面积;
(3)当四边形PQBC的面积等于14时,求t的值.
(4)当t为何值时,△PBQ是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011年江苏省苏州市中考模拟数学卷 题型:解答题
(本题9分)如图,已知抛物线y=ax2+bx+3的图象与x轴交于A、B两点,与y轴交于点C,且点C、D是抛物线上的一对对称点.
【小题1】(1)求抛物线的解析式;
【小题2】(2)求点D的坐标,并在图中画出直线BD;
【小题3】(3)求出直线BD的一次函数解析式,并根据图象回答:当x满足什么条件时,上述二次函数的值大于该一次函数的值.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年苏州工业园区九年级下学期学科调研数学卷 题型:解答题
(9分)如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C.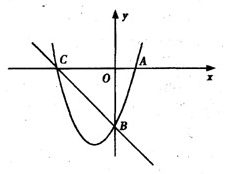
(1)求抛物线的解析式;
(2)若在第三象限的抛物线上存在点P,使△PBC为以点B为直角顶点的直角三角形,
求点P的坐标;
(3)在(2)的条件下,在抛物线上是否存在一点Q,使以P,Q,B,C为顶点的四边形
为直角梯形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年陕西省兴平市九年级上学期期末练习数学卷 题型:解答题
(本题满分10分)
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(—1,0)、C(0,—3)两点,与x轴交于另一点B.
1.(1)求这条抛物线所对应的函数关系式;
2.(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标;
3.(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com