
【题目】计算与化简:
(1)12﹣(﹣6)+(﹣9)
(2)(﹣1)2016+(﹣4)2÷(﹣ ![]() )+|﹣1﹣2|
)+|﹣1﹣2|
(3)先化简,再求值:﹣ ![]() (4a2+2a﹣2)+(a﹣1),其中a=
(4a2+2a﹣2)+(a﹣1),其中a= ![]()
(4)点P在数轴上的位置如图所示,化简:|p﹣1|+|p﹣2| ![]()
【答案】
(1)解:原式=12+6﹣9=18﹣9=9
(2)解:原式=1﹣12+3=4﹣12=﹣8
(3)解:原式=2a2﹣a+1+a﹣1=﹣2a2,
当x= ![]() 时,原式=﹣2×
时,原式=﹣2× ![]() =﹣
=﹣ ![]()
(4)解:由图可知:p﹣1>0,p﹣2<0,
则|p﹣1|+|p﹣2|=(p﹣1)﹣(p﹣2)=p﹣1﹣p+2=1
【解析】(1)原式利用减法法则变形,计算即可得到结果;(2)原式第一项利用乘方的意义化简,第二项利用乘方的意义及除法法则变形,最后一项利用绝对值的代数意义化简,计算即可得到结果;(3)原式去括号合并得到最简结果,把a的值代入计算即可求出值;(4)根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,去括号合并即可得到结果.
【考点精析】本题主要考查了数轴和有理数的四则混合运算的相关知识点,需要掌握数轴是规定了原点、正方向、单位长度的一条直线;在没有括号的不同级运算中,先算乘方再算乘除,最后算加减才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD. 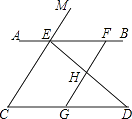
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.
(1)已知点A的坐标为(1,0),
①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)正方形RSKT顶点R的坐标为(-1,1),K的坐标为(2,-2),点M的坐标为(m,3),若在正方形RSKT边上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
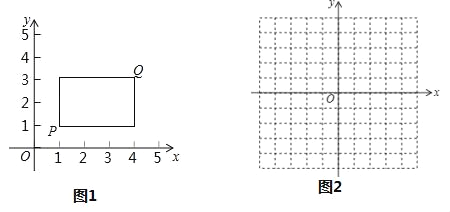
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在给定的条件中,能作出平行四边形的是( )
A. 以60cm为对角线,20cm、34cm为两条邻边
B. 以20cm、36cm为对角线,22cm为一条边
C. 以6cm为一条对角线,3cm、10cm为两条邻边
D. 以6cm、10cm为对角线,8cm为一条边
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,l1反映了某公司的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量( ) 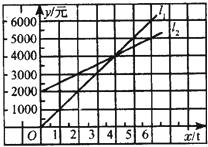
A.小于3t
B.大于3t
C.小于4t
D.大于4t
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个宾馆有二人间、三人间、四人间三种客房供游客租住,某旅行团25人准备同时租用这三种客房共9间,如果每个房间都住满,则租房方案共有( )
A.4种
B.3种
C.2种
D.1种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com