
| 购票人数 | 1~49人 | 50~100人 | 100人以上 |
| 每人门票价 | 130元 | 110元 | 90元 |
分析 (1)设这两个旅游团共有m人,分50<m≤100和m>100两种情况,列出关于m的一元一次方程,解之取其正整数即可得出结论;
(2)设甲旅游团有x人,乙旅游团有y人,分x≥y>50和x>50≥y两种情况,列出关于x、y的二元一次方程组,解之即可得出结论.
解答 解:(1)设这两个旅游团共有m人,
当50<m≤100时,有110m=10080,
解得:m≈91.64(不为整数,舍去);
当m>100时,有90m=10080,
解得:m=112.
答:这两个旅游团共有112人.
(2)设甲旅游团有x人,乙旅游团有y人,
当x≥y>50时,有$\left\{\begin{array}{l}{x+y=112}\\{110(x+y)=13140}\end{array}\right.$,
方程组无解;
当x>50≥y时,有$\left\{\begin{array}{l}{x+y=112}\\{110x+130y=13140}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=71}\\{y=41}\end{array}\right.$.
答:甲旅游团有71人,乙旅游团有41人.
点评 本题考查了二元一次方程组的应用以及一元一次方程的应用,解题的关键是:(1)分50<m≤100和m>100两种情况,列出关于m的一元一次方程;(2)分x≥y>50和x>50≥y两种情况,列出关于x、y的二元一次方程组.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
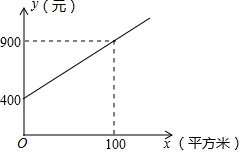 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
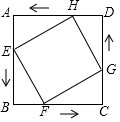 如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为3s时,四边形EFGH的面积最小,其最小值是18cm2.
如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为3s时,四边形EFGH的面积最小,其最小值是18cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
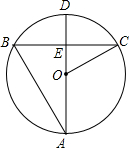 如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC的长为( )
如图,AD是⊙O的直径,弦BC⊥AD于E,AB=BC=12,则OC的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com