
【题目】一艘渔船从港口A沿北偏东60°方向航行至C处时突然发生故障,在C处等待救援.有一救援艇位于港口A正东方向20(![]() ﹣1)海里的B处,接到求救信号后,立即沿北偏东45°方向以30海里/小时的速度前往C处救援.则救援艇到达C处所用的时间为( )
﹣1)海里的B处,接到求救信号后,立即沿北偏东45°方向以30海里/小时的速度前往C处救援.则救援艇到达C处所用的时间为( )

A. ![]() 小时 B.
小时 B. ![]() 小时 C.
小时 C. ![]() 小时 D.
小时 D. ![]() 小时
小时
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,BD是中线,AF⊥BD,F为垂足,过点C作AB的平行线交AF的延长线于点E.

求证:(1)∠ABD=∠FAD;(2)AB=2CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①,②分别是根据某地近两年6月上旬日平均气温情况绘制的折线统计图,通过观察图表回答:

去年6月上旬①

今年6月上旬②
(1)该地这两年6月上旬日平均气温分别是多少?
(2)该地这两年6月上旬日平均气温的极差分别是多少?由此可以判断哪一年6月上旬气温比较稳定?
折线图能直观地反映数据的变化趋势,能比较容易地看出变动范围,求出极差,运用时还要注意观察,通过纵横坐标的交点寻找所需要的数据信息,根据信息和题目要求作出正确分析.
观察图可知去年6月上旬的日平均气温(单位:℃)分别是:24,30,29,24,23,26,27,26,30,26.由图可知今年6月上旬的日平均气温(单位 ℃)分别是:24,26,25,26,24,26,27,26,27,26.然后求这两年的平均气温及极差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形OABC的顶点A在x轴上,OA=4,OC=3,点D为BC边上一点,以AD为一边在与点B的同侧作正方形ADEF,连接OE.当点D在边BC上运动时,OE的长度的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;
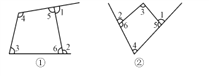
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
如图,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com