
����Ŀ���ҹ��ж����������������������أ����������ѿ̲��ݻ�������ij�����̳��������ڽ�����Ҫ����������ij�ּ��ÿ������������������200Ԫ/̨�������г����ۺ��֣���һ�����ڣ����ۼ���400Ԫ/̨ʱ�����۳�200̨�����ۼ�ÿ����10Ԫ���Ϳɶ��۳�50̨���������̹涨���ֿ����������ۼ۲��ܵ���300Ԫ/̨������������ÿ��Ҫ��ɲ�����450̨����������
��1����ȷ����������y��̨�����ۼ�x��Ԫ/̨��֮��ĺ�����ϵʽ��
��2�����ۼ�x�ķ�Χ��
��3�����ۼ�x��Ԫ/̨����Ϊ����ʱ���̳�ÿ���������ֿ�������������õ�����w��Ԫ�������������Ƕ��٣�
���𰸡���1����������y��̨�����ۼ�x��Ԫ/̨��֮��ĺ�����ϵʽΪy=��5x+2200��
��2��x�ķ�Χ��300��x��350��
��3���ۼ۶�Ϊ320Ԫ/̨ʱ���̳�ÿ���������ֿ�������������õ�����w������������72000Ԫ��
�����������������(1)��������=200+50��(���۵�������10)�ó��𰸣�(2)�����ݹ����̹涨���ֿ����������ۼ۲��ܵ���300Ԫ/̨������������ÿ��Ҫ��ɲ�����450̨���ó�����ʽ�飬�Ӷ��ó�x��ȡֵ��Χ��(3)������������=��������������ó�������ϵʽ��Ȼ����ݶ��κ��������ʵó����ֵ.
���������(1)�����������������ۼ�ÿ����10Ԫ�����������Ϳɶ��۳�50̨��
����������y��̨�����ۼ�x��Ԫ/̨��֮��ĺ�����ϵʽ��y=200+50��![]() ��
��
����ã�y=-5x+2200��
(2)�����ݹ����̹涨���ֿ����������ۼ۲��ܵ���300Ԫ/̨������������ÿ��Ҫ��ɲ�����450̨�� ��x��300��5x+2200��450
��ã�300��x��350��
����y��x֮��ĺ�����ϵʽΪ��y=-5x+2200��300��x��350����
(3)��W=��x-200����-5x+2200���� �����ã�W=-5![]() +72000��
+72000��
��x=320��300��x��350�ڣ� �൱x=320ʱ�����ֵΪ72000��
���ۼ۶�Ϊ320Ԫ/̨ʱ���̳�ÿ���������ֿ�������������õ�����w������������72000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=![]() ��x��4���������ཻ��A��B��C���㣬P���߶�AB��һ���㣨�˵���⣩����P��PD��AC����BC�ڵ�D������CP��
��x��4���������ཻ��A��B��C���㣬P���߶�AB��һ���㣨�˵���⣩����P��PD��AC����BC�ڵ�D������CP��
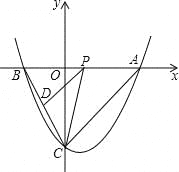
��1��ֱ��д��A��B��C�����ꣻ
��2����������y=![]() ��x��4�ĶԳ���Ͷ������ꣻ
��x��4�ĶԳ���Ͷ������ꣻ
��3������PCD��������ֵ�����жϵ���PCD�����ȡ���ֵʱ����PA��PDΪ�ڱߵ�ƽ���ı����Ƿ�Ϊ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
����������˵��������ʲô���ӣ��Ҳ����ã������ҵ������ȥ�жϣ���ƽ֮��������ã�����ժ�ԡ�ס���Ρ������ɫ������ҶΪ����������ɫ���٣�
С��Ҹ���������һ�ι�·�����������д�ţ�������·�����������������������ðְֿ���ʻ����ι�·�������ٶ�Ϊ60ǧ��/Сʱ������Լ3���ӣ��ɴ˹������·��Լǧ�ף�
Ȼ��С��������ϣ���֪����Ϊ��Ҷ����ľ����������������ֱ���ɴ�8�ף�С��ƻ���·����㿪ʼ��ÿa����һ����������ʾ��ͼ���£�
���ǵ�Ͷ���ʽ�����ƣ����������һ�ַ�������ԭ�ƻ���a����һ������·������Ƽ���200�������������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˳�������ı���ABCD���ߵ��е������ı����Ǿ��Σ����ı���ABCDһ���ǣ� ��
A.����
B.����
C.�Խ����ഹֱ���ı���
D.�Խ�����ȵ��ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˳�������ı���ABCD���ߵ��е������ı����Ǿ��Σ����ı���ABCDһ���ǣ� ��
A.����
B.����
C.�Խ����ഹֱ���ı���
D.�Խ�����ȵ��ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�����Σ��Խ���AC��BD�ཻ�ڵ�O��DH��AB��H�� ����OH����֤����DHO=��DCO��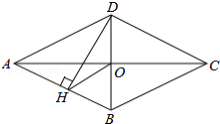
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1=��2����B=��C�����Ƶ�AB��CD���������£�
�ߡ�1=��2����֪����
�ҡ�1=��CGD����
���2=��CGD������������
��CE��BF����
���=��BFD����
�֡ߡ�B=��C����֪��
���BFD=��B������������
��AB��CD����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com