
【题目】如图,在矩形ABCD中,AD= ![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;
②OE=OD;
③BH=HF;
④BC﹣CF=2HE;
⑤AB=HF.
其中正确的有( )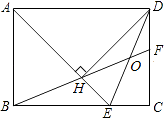
A.①②③④⑤
B.①②③④
C.①③④⑤
D.①②③⑤
【答案】B
【解析】解:∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AE= ![]() AB,
AB,
∵AD= ![]() AB,
AB,
∴AE=AD,
在△ABE和△AHD中,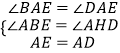
∴△ABE≌△AHD(AAS),
∴BE=DH,
∴AB=BE=AH=HD,
∴∠ADE=∠AED= ![]() (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠CED=180°﹣45°﹣67.5°=67.5°,
∴∠AED=∠CED,故①正确;
∵AB=AH,
∵∠AHB= ![]() (180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),
(180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),
∴∠OHE=67.5°=∠AED,
∴OE=OH,
∵∠DHO=90°﹣67.5°=22.5°,∠ODH=67.5°﹣45°=22.5°,
∴∠DHO=∠ODH,
∴OH=OD,
∴OE=OD=OH,故②正确;
∵∠EBH=90°﹣67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,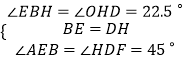
∴△BEH≌△HDF(ASA),
∴BH=HF,HE=DF,故③正确;
∵HE=AE﹣AH=BC﹣CD,
∴BC﹣CF=BC﹣(CD﹣DF)=BC﹣(CD﹣HE)=(BC﹣CD)+HE=HE+HE=2HE.故④正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故⑤错误;
综上所述,结论正确的是①②③④,
故选B.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,作出函数 ![]() 的图象,并根据图象回答下列问题:
的图象,并根据图象回答下列问题: 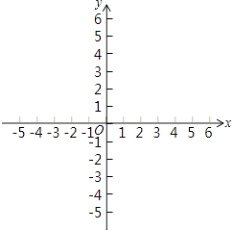
(1)当x=﹣2时,求y的值;
(2)当2<y<4时,求x的取值范围;
(3)当﹣1<x<2,且x≠0时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
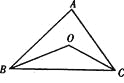
【题目】如图,在△ ABC中,∠ ABC、∠ ACB的平分线交于点O。
(1)若∠ABC=40°,∠ ACB=50°,则∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°,则∠BOC="________"
(3)若∠A=70°,则∠BOC=_________
(4)若∠BOC=140°,则∠A=________
(5)你能发现∠ BOC与∠ A之间有什么数量关系吗?写出并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全解题过程.
如图所示,点C是线段AB的中点,点D在线段AB上,且AD=![]() DB.若AC=3,求线段DC的长.
DB.若AC=3,求线段DC的长.
![]()
解:∵ 点C是线段AB的中点,(已知)
∴ AB=2 AC .( )
∵AC=3,(已知)
∴ AB= .
∵点D在线段AB上,AD=![]() DB,(已知)
DB,(已知)
∴ AD= AB,∴ AD= ,∴DC= - AD = .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学在将一张矩形纸片ABCD的四个角向内折起时,发现恰好能拼成一个无缝隙无重叠的四边形EFGH.于是他测量出EH=12cm,EF=16cm,根据这两个数据他很快求出了边AD的长,则边AD的长是( ) 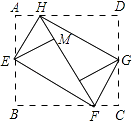
A.12cm
B.16cm
C.20cm
D.28cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图. 根据上述信息,解答下列问题:

(1)本次抽取的学生人数是 ______ ;扇形统计图中的圆心角α等于 ______ ;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点.
![]() 若点D在线段CB上,且DB=2cm,AD=8cm,求线段CD的长度;
若点D在线段CB上,且DB=2cm,AD=8cm,求线段CD的长度;
![]() 若将
若将![]() 中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其它条件不变,请画出相应的示意图,并求出此时线段CD的长度.
中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其它条件不变,请画出相应的示意图,并求出此时线段CD的长度.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com