【题目】已知⊙O的直径长为10，弦AB长为8，弦长CD为6，且AB∥CD，则弦AB与CD之间的距离为_______.
【答案】1或7
【解析】
连接OA，OC，作直线EF⊥AB于E，交CD于F，由AB∥CD，根据垂径定理得到AE=
AB=3，CF=CD=4，再根据勾股定理可计算出OF=4，OE=3，然后分类讨论：当AB和CD在圆心的同侧时，则EF=OF-OE；②当AB和CD在圆心的两侧时，则EF=OE+OF．
解：如图所示，连接OA，OC．作直线EF⊥AB于E，交CD于F，
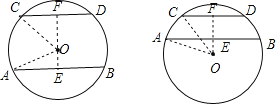
∵AB∥CD，
∴EF⊥CD．
∵OE⊥AB，OF⊥CD，
∴AE=AB=3，CF=CD=4，
①当AB和CD在圆心的同侧时，则EF=OF-OE=1；
②当AB和CD在圆心的两侧时，则EF=OE+OF=7．
则AB与CD间的距离为1或7．
故答案为1或7.
科目：初中数学 来源： 题型：
【题目】“端午节”又称为端阳节、重午节、龙舟节、正阳节、洛兰节等，是中国四大传统节日之一，端午习俗众多，其中吃粽子是端午节的习俗主题之一，某超市5月以50元/盒的进价购进一款粽子1000盒，以100元/盒的售价全部销售完.销售人员根据市场调研预测，该款粽子每盒的售价在5月售价基础上每降价5元，月销量就会相应增加100盒，该超市6月计划购进该款粽子不超过1400盒.
（1）根据该超市6月计划，该款粽子6月的售价最少每盒可以定价多少元？
（2）实际上，6月该超市购进该款粽子的进价比5月便宜了
元，而实际售价在5月基础上降了m元，已知6月的销售利润比5月增加8%，求m的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y＝ax2+bx+c（a≠0）与x轴交于A，B两点，与y轴交于点C，点B，C的坐标分别为（4，0）和（0，4），抛物线的对称轴为x＝1，直线AD交抛物线于点D（2，m）．
（1）求抛物线和直线AD的解析式；
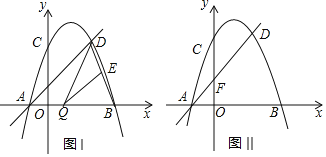
（2）如图Ⅰ，点Q是线段AB上一动点，过点Q作QE∥AD，交BD于点E，连接DQ，求△QED面积的最大值；
（3）如图Ⅱ，直线AD交y轴于点F，点M，N分别是抛物线对称轴和抛物线上的点，若以C，F，M，N为顶点的四边形是平行四边形，求点M的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
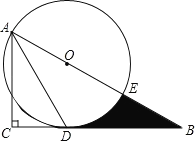
【题目】如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．以AB上某一点O为圆心作⊙O，使⊙O经过点A和点D．
（1）判断直线BC与⊙O的位置关系，并说明理由；
（2）若AC=3，∠B=30°．
①求⊙O的半径；
②设⊙O与AB边的另一个交点为E，求线段BD、BE与劣弧DE所围成的阴影部分的图形面积．（结果保留根号和π）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某单位要建一个面积为48 m2的小仓库，小仓库有一边靠墙(墙长10m)，并在与墙平行的一边开一道宽1 m的门，现有能围成19 m的木板，求小仓库的长与宽？
(注意：仓库靠墙的那一边不能超过墙长)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明将小球沿地面成一定角度的方向击出，在不考虑空气阻力的条件下，小球的飞行高度y（m）与它的飞行时间x（s）满足二次函数关系，y与x的几组对应值如表所示：
（1）求y关于x的函数解析式（不要求写x的取值范围）；
（2）问：小球的飞行高度能否达到20.5m？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市去年成功举办2018郴州国际休闲旅游文化节，获评“全国森林旅游示范市”．某市有A，B，C，D，E五个景区很受游客喜爱．一旅行社对某小区居民在暑假期间去以上五个景区旅游（只选一个景区）的意向做了一次随机调查统计，并根据这个统计结果制作了如下两幅不完整的统计图：
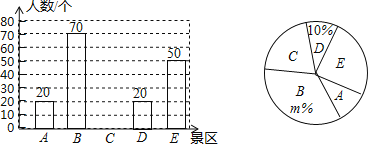
（1）该小区居民在这次随机调查中被调查到的人数是 人，
，并补全条形统计图；
（2）若该小区有居民1200人，试估计去B地旅游的居民约有多少人？
（3）小军同学已去过E地旅游，暑假期间计划与父母从A，B，C，D四个景区中，任选两个去旅游，求选到A，C两个景区的概率．（要求画树状图或列表求概率）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为⊙O直径，C是⊙O上一点，CO⊥AB于点O，弦CD与AB交于点F，在AB的延长线上取一点E，使EF＝ED，过点A作⊙O的切线交ED的延长线于点G.
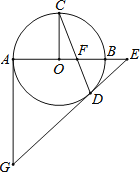
（1）求证：GE是⊙O的切线；
（2）若OF：OB＝1：3，⊙O的半径为3，求DE和AG的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
