
【题目】如图,在ABCD中,AE=CG,BF=DH,连接EF,FG,GH,HE.求证:四边形EFGH是平行四边形. 
 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】下列结论错误的是( )
A.垂直于同一直线的两条直线互相平行
B.两直线平行,同旁内角互补
C.过直线外一点有且只有一条直线与这条直线平行
D.同一平面内,不相交的两条直线叫做平行线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,连接BD.
(1)如图1,AE⊥BD于E.直接写出∠BAE的度数.
(2)如图1,在(1)的条件下,将△AEB以A旋转中心,沿逆时针方向旋转30°后得到△AB′E′,AB′与BD交于M,AE′的延长线与BD交于N.


①依题意补全图1;
②用等式表示线段BM、DN和MN之间的数量关系,并证明.
(3)如图2,E、F是边BC、CD上的点,△CEF周长是正方形ABCD周长的一半,AE、AF分别与BD交于M、N,写出判断线段BM、DN、MN之间数量关系的思路.(不必写出完整推理过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和反射出的光线与平面镜所夹的角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射出去,若b镜反射出的光线n平行于m,且∠1=30![]() ,则∠2= ,∠3= ;
,则∠2= ,∠3= ;
(2)在(1)中,若∠1=70![]() ,则∠3= ;若∠1=a,则∠3= ;
,则∠3= ;若∠1=a,则∠3= ;
(3)由(1)(2)请你猜想:当∠3= 时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的?请说明理由.
(提示:三角形的内角和等于180![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
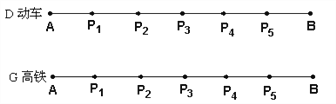
【题目】以下是两张不同类型火车的车票(“![]() 次”表示动车,“
次”表示动车,“![]() 次”表示高铁):
次”表示高铁):

(1)根据车票中的信息填空:该列动车和高铁是__________向而行(填“相”或“同”).
(2)已知该列动车和高铁的平均速度分别为![]() 、
、![]() ,两列火车的长度不计.
,两列火车的长度不计.
①经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到![]() ,求
,求![]() 、
、![]() 两地之间的距离.
两地之间的距离.
②在①中测算的数据基础上,已知![]() 、
、![]() 两地途中依次设有
两地途中依次设有![]() 个站点
个站点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,动车每个站点都停靠,高铁只停靠
,动车每个站点都停靠,高铁只停靠![]() 、
、![]() 两个站点,两列火车在每个停靠站点都停留
两个站点,两列火车在每个停靠站点都停留![]() .求该列高铁追上动车的时刻.
.求该列高铁追上动车的时刻.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学连续观察了太原市2014年8月份某几天的天气情况,他的观察结果是:①共有5个下午是晴天;②共有7个上午是晴天;③共有8个半天是雨天;④下午下雨的那天上午是晴天,则该学生观察的天数为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com