
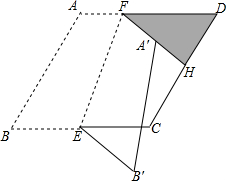
 已知菱形ABCD,AB=2,∠ABC=60°,E为BC的中点,点F为边AD上一点,以EF为折痕将四边形ABEF折叠得到四边形A′B′EF.
已知菱形ABCD,AB=2,∠ABC=60°,E为BC的中点,点F为边AD上一点,以EF为折痕将四边形ABEF折叠得到四边形A′B′EF.分析 (1)连接AE、AC,根据等边三角形的性质和等腰三角形的三线合一解答;
(2)连接EA、EA′,作CG⊥FH于G,设DH=x,根据直角三角形的性质用x表示出FD、AF、根据矩形的性质以及翻转变换的性质解答即可.
解答 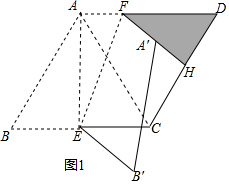 解:(1)连接AE、AC,
解:(1)连接AE、AC,
∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,又E为BC的中点,
∴AE⊥BC,
∵AD∥BC,
∴∠EAF=90°,
故答案为:90°;
(2)连接EA、EA′,作CG⊥FH于G,
∵∠DHF=90°,∠D=60°,
∴∠DFH=30°,
设DH=x,则FD=2x,AF=2-2x,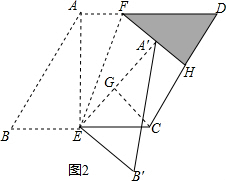
由翻转变换的性质可知,A′F=AF=2-2x,
由勾股定理得,FH=$\sqrt{3}$x,则A′H=($\sqrt{3}$+2)x-2,
∵∠DFH=30°,
∴∠AFH=150°,
∴∠AEA′=30°,
∴∠GEC=60°,
∴∠ECG=30°,又EC=$\frac{1}{2}$BC=1,
∴CG=$\frac{\sqrt{3}}{2}$,
∵四边形CGA′H是矩形,
∴$\frac{\sqrt{3}}{2}$=($\sqrt{3}$+2)x-2,
解得,x=$\frac{5}{2}$-$\sqrt{3}$,
则DF=2x=5-2$\sqrt{3}$.
故答案为:5-2$\sqrt{3}$.
点评 本考查的是翻转变换的性质,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
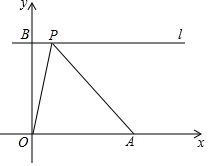 如图,在平面直角坐标系中,点A的坐标为(5,0),点B的坐标为(0,4),过点B作直线l平行x轴,点P在直线l上运动.设点P的横坐标为a,记点B关于直线OP的对称点为B′,若点B′落在△OAP内部(不包括边上),则a的取值范围为2<a<4.
如图,在平面直角坐标系中,点A的坐标为(5,0),点B的坐标为(0,4),过点B作直线l平行x轴,点P在直线l上运动.设点P的横坐标为a,记点B关于直线OP的对称点为B′,若点B′落在△OAP内部(不包括边上),则a的取值范围为2<a<4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com