
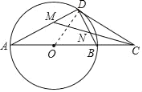
【题目】如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.
(1)求证:直线CD是⊙O的切线;
(2)若CM平分∠ACD,且分别交AD,BD于点M,N,当DM=2时,求MN的长.

【答案】(1)见解析;(2)MN=2![]() .
.
【解析】
(1)如图,连接OD.欲证明直线CD是⊙O的切线,只需求得∠ODC=90°即可;
(2)由角平分线及三角形外角性质可得∠A+∠ACM=∠BDC+∠DCM,即∠DMN=∠DNM,根据勾股定理可求得MN的长.
(1)证明:如图,连接OD.
∵AB为⊙O的直径,
∴∠ADB=90°,即∠A+∠ABD=90°,
又∵OD=OB,
∴∠ABD=∠ODB,
∵∠A=∠BDC;
∴∠CDB+∠ODB=90°,即∠ODC=90°.
∵OD是圆O的半径,
∴直线CD是⊙O的切线;
(2)解:∵CM平分∠ACD,
∴∠DCM=∠ACM,
又∵∠A=∠BDC,
∴∠A+∠ACM=∠BDC+∠DCM,即∠DMN=∠DNM,
∵∠ADB=90°,DM=2,
∴DN=DM=2,
∴MN=![]() =2
=2![]() .
.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.了解全市中学生对社会主义核心价值观的知晓度的情况,适合用抽样调查
B.若甲组数据方差S2甲=0.39,乙组数据方差S2乙=0.27,则乙组数据比甲组数据稳定
C.某种彩票中奖的概率是![]() ,买100张该种彩票一定会中奖
,买100张该种彩票一定会中奖
D.旅客上飞机前的安检应该进行全面调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() 、
、![]() .
.
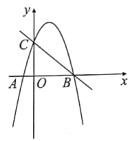
(1)求抛物线的表达式;
(2)过点![]() 的直线
的直线![]() 交抛物线于点
交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,当直线
,当直线![]() 平分
平分![]() 的面积时,求点
的面积时,求点![]() 的坐标;
的坐标;
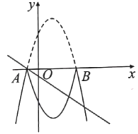
(3)如图所示,把抛物线位于![]() 轴上方的图象沿
轴上方的图象沿![]() 轴翻折,当直线
轴翻折,当直线![]() 与翻折后的整个图象只有三个交点时,求
与翻折后的整个图象只有三个交点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
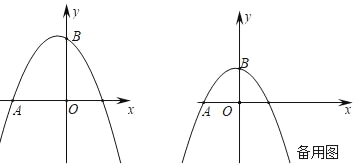
【题目】已知抛物线y=ax2﹣![]() x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
(1)求抛物线的解析式;
(2)当BQ=![]() AP时,求t的值;
AP时,求t的值;
(3)随着点P,Q的运动,抛物线上是否存在点M,使△MPQ为等边三角形?若存在,请求出t的值及相应点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=2,则图中阴影部分的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为迎接县中学生篮球比赛,计划购买A、B两种篮球共20个供学生训练使用.若购买A种篮球6个,则购买两种篮球共需费用720元;若购买A种篮球12个,则购实两种篮球共需费用840元.
(1)A、B两种篮球共需单价各多少元?
(2)设购买A种篮球x个且A种篮球不少于8个,所需费用为y元,试确定y与x的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
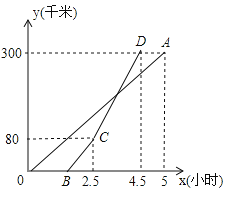
【题目】如图:甲、乙两地相距![]() ,一辆货车和一辆轿车先后从甲地出发驶向乙地,线段
,一辆货车和一辆轿车先后从甲地出发驶向乙地,线段![]() 和折线
和折线![]() 分别表示货车和轿车离甲地的距离
分别表示货车和轿车离甲地的距离![]()
![]() 与货车出发时间
与货车出发时间![]()
![]() 之间的函数关系,请根据图象解答下列问题:
之间的函数关系,请根据图象解答下列问题:
(1)货车的速度为___________![]() ,当轿车到达乙地后,货车距乙地的距离为____________千米;
,当轿车到达乙地后,货车距乙地的距离为____________千米;
(2)求轿车改变速度后![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)轿车到达乙地后,马上沿原路以![]() 段速度返回,求轿车从乙地出发后多长时间再次与货车相遇?
段速度返回,求轿车从乙地出发后多长时间再次与货车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线.
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求点B到AC的距离.
,求点B到AC的距离.
(3)在第(2)的条件下,求△ACP的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com