
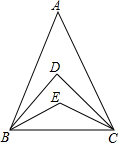
 如图,在△ABC中,∠A=50°,E是△ABC内一点,∠BEC=150°,∠ABE的平分线与∠ACE的平分线相交于点D,则∠BDC的度数为多少?
如图,在△ABC中,∠A=50°,E是△ABC内一点,∠BEC=150°,∠ABE的平分线与∠ACE的平分线相交于点D,则∠BDC的度数为多少? 分析 先根据∠A=50°求出∠ABC+∠ACB的度数,再根据∠BEC=150°求出∠EBC+∠ECB的度数,由此可得出∠ABE+∠ACE的度数,根据角平分线的性质可得出∠DBE+∠DCE的度数,由三角形内角和定理即可得出结论.
解答 解:∵△ABC中∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,
∵△BCE中∠E=150°,
∴∠EBC+∠ECB=180°-150°=30°,
∴∠ABE+∠ACE=130°-30°=100°,
∵∠ABE的平分线与∠ACE的平分线相交于点D,
∴∠DBE+∠DCE=$\frac{1}{2}$(∠ABE+∠ACE)=$\frac{1}{2}$×100°=50°,
∴∠DBE+∠DCE=(∠DBE+∠DCE)+(∠EBC+∠ECB)=50°+30°=80°,
∴∠BDC=180°-80°=100°.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
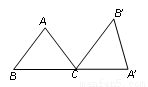
如图,在△ABC中,AB=AC =5,BC=6,将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C,若点A′恰好落在BC的延长线上,则点B′到BA′的距离为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )
把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是( )| A. | $\left\{\begin{array}{l}{x>-1}\\{x≤2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x≥-1}\\{x<2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x≥-1}\\{x≤2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<-1}\\{x≥2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
如图,在△ABC中,按以下步骤作图:①分别以点B,C为圆心,以大于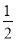 BC的长为半径作弧,两弧交于M,N两点;②作直线MN交AB于点D,连接CD.如果已知CD=AC,∠B=25°,则∠ACB的度数为__________.
BC的长为半径作弧,两弧交于M,N两点;②作直线MN交AB于点D,连接CD.如果已知CD=AC,∠B=25°,则∠ACB的度数为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 事件M为不可能事件 | B. | 事件M为必然事件 | ||
| C. | 事件M发生的概率为$\frac{1}{4}$ | D. | 事件M发生的概率为$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com