
【题目】小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | a | 40% |
1200≤x<1400 | 9 | 22.5% |
1400≤x<1600 | b | c |
1600≤x<1800 | 2 | 5% |
合计 | 40 | 100% |
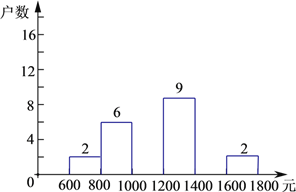
根据以上提供的信息,解答下列问题:
(1)频数分布表中:a= ,b= ,c= .
(2)补全频数分布直方图.
(3)请估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
【答案】(1)16,5,12.5%;(2)补图见解析;(3)420户
【解析】(1)(2)根据600≤x<800一组频数是2,所占的百分比是5%即可求得总人数,然后根据百分比的意义求得a、b、c的值,从而补全统计表和频数分布直方图;
(3)利用总人数560乘以对应的百分比即可求解.
解:(1)
调查的总户数是2÷5%=40(户),
则收入是1000x<1200一组的人数是:a=40×40%=16(人),
1400≤x<1600这一组的人数是:b=40-2-6-16-9-2=5(人),
所占百分比为c=![]()
故答案为:a= 16,b= 5,c=12.5%
(2)如图所示:
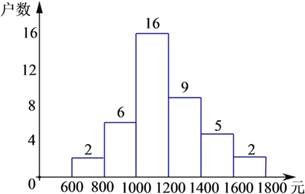
(3)![]() (户)
(户)
答:估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有420户.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】把方程3x(x+1)=2(x–2)+8化为一般形式______,二次项系数______,一次项系数__________,常数项______。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”。
(1)请问一元二次方程x2-3x+2=0是倍根方程吗?如果是,请说明理由。
(2)若一元二次方程ax2+bx-6=0是倍根方程,且方程有一个根为2,求a、b的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
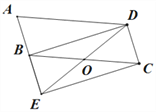
【题目】如图,将□ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.
(1)求证:四边形BECD是平行四边形;
(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
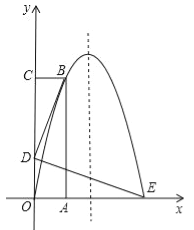
【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
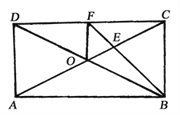
【题目】如图,已知矩形ABCD的对角线AC、BD交于O点,∠ABC的平分线交AC于E,交CD于F,∠DBF=15°,连结OF,则下列三角形①△AOD,②△COF,③△DOF,④△EOF中是等腰三角形的为________(填入序号)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com