
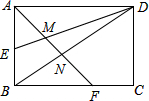
 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为$\frac{9}{20}\sqrt{2}$.
如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为$\frac{9}{20}\sqrt{2}$. 分析 首先过F作FH⊥AD于H,交ED于O,于是得到FH=AB=2,根据勾股定理求得AF,根据平行线分线段成比例定理求得OH,由相似三角形的性质求得AM与AF的长,根据相似三角形的性质,求得AN的长,即可得到结论.
解答 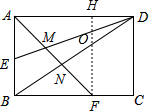 解:过F作FH⊥AD于H,交ED于O,则FH=AB=2
解:过F作FH⊥AD于H,交ED于O,则FH=AB=2
∵BF=2FC,BC=AD=3,
∴BF=AH=2,FC=HD=1,
∴AF=$\sqrt{F{H}^{2}+A{H}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∵OH∥AE,
∴$\frac{HO}{AE}$=$\frac{DH}{AD}$=$\frac{1}{3}$,
∴OH=$\frac{1}{3}$AE=$\frac{1}{3}$,
∴OF=FH-OH=2-$\frac{1}{3}$=$\frac{5}{3}$,
∵AE∥FO,
∴△AME∽FMO,
∴$\frac{AM}{FM}$=$\frac{AE}{FO}$=$\frac{3}{5}$,
∴AM=$\frac{3}{8}$AF=$\frac{3\sqrt{2}}{4}$,
∵AD∥BF,
∴△AND∽△FNB,
∴$\frac{AN}{FN}$=$\frac{AD}{BF}$=$\frac{3}{2}$,
∴AN=$\frac{3}{5}$AF=$\frac{6\sqrt{2}}{5}$,
∴MN=AN-AM=$\frac{6\sqrt{2}}{5}$-$\frac{3\sqrt{2}}{4}$=$\frac{9\sqrt{2}}{20}$.
故答案为:$\frac{9}{20}\sqrt{2}$.
点评 本题考查了相似三角形的判定与性质,矩形的性质,勾股定理,比例的性质,准确作出辅助线,求出AN与AM的长是解题的关键.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,点P是x轴上的一个动点,连结AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.当点P运动到点($\sqrt{3}$,0)时,则点D的坐标为(2$\sqrt{3}$,3).
如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,点P是x轴上的一个动点,连结AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.当点P运动到点($\sqrt{3}$,0)时,则点D的坐标为(2$\sqrt{3}$,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| (1)-150+250; | (2)-15+(-23); |
| (3)-5-65; | (4)-26-(-15); |
| (5)-6×(-16); | (6)-$\frac{1}{3}$×27; |
| (7)8÷(-16); | (8)-25÷(-$\frac{2}{3}$); |
| (9)(-0.02)×(-20)×(-5)×4.5; | (10)(-6.5)×(-2)÷(-$\frac{1}{3}$)÷(-5); |
| (11)6+(-$\frac{1}{5}$)-2-(-1.5); | (12)-66×4-(-2.5)÷(-0.1); |
| (13)(-2)2×5-(-2)3÷4; | (14)-(3-5)+32×(1-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
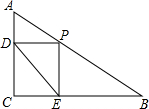 如图,在Rt△ABC中,∠ACB=90°.AC=3,BC=4,P为AB边上一点;且PD⊥AC于D,PE⊥BC于E,则DE的最小值为$\frac{12}{5}$.
如图,在Rt△ABC中,∠ACB=90°.AC=3,BC=4,P为AB边上一点;且PD⊥AC于D,PE⊥BC于E,则DE的最小值为$\frac{12}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com