
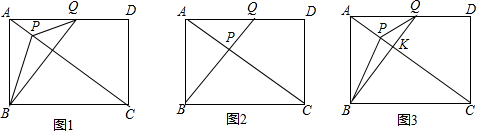
���� ��1����Rt��ABQ�У����AQ�����ù��ɶ����������BQ��
��2����ֱ�����������PA��DQ��ֵ���ɽ�����⣻
��3����ͼ3�У���PM��AD��M��PN��AB��N����PM=$\frac{3}{5}$x��PN=$\frac{4}{5}$x���������B��P��Q����ʱx��ֵ�����������ηֱ���⼴�ɣ�
��� �⣺��1����ͼ1�У�
���ı���ABCD�Ǿ��Σ�
��AD=BC=8����BAD=90�㣬
��QD=2AP��AP=1��
��DQ=2��AQ=6��
��Rt��ABQ��BQ=$\sqrt{A{B}^{2}+A{Q}^{2}}$=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$��
��2����ͼ2�У�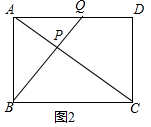
��Rt��ABC��AC=$\sqrt{{6}^{2}+{8}^{2}}$=10��
��$\frac{1}{2}$•AB•BC=$\frac{1}{2}$•AC•BP��
��PB=$\frac{6��8}{10}$=$\frac{24}{5}$��
��PA=$\sqrt{A{B}^{2}-B{P}^{2}}$=$\frac{18}{5}$��
��PC=AC-AP=$\frac{32}{5}$��
��AQ��BC��
��$\frac{AQ}{BC}$=$\frac{AP}{PC}$��
��$\frac{AQ}{8}$=$\frac{\frac{18}{5}}{\frac{32}{5}}$��
��AQ=$\frac{9}{2}$��
��DQ=8-$\frac{9}{2}$=$\frac{7}{2}$��
��$\frac{7}{2}$=k•$\frac{18}{5}$��
��k=$\frac{35}{36}$��
��3����ͼ3�У���PM��AD��M��PN��AB��N����PM=$\frac{3}{5}$x��PN=$\frac{4}{5}$x��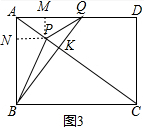
��DQ��8��
��2x��8��
��0��x��4��
��B��P��Q����ʱ��$\frac{8-2x}{8}$=$\frac{x}{10-x}$���x=18-2$\sqrt{61}$��18+2$\sqrt{61}$����������
�൱0��x��18-2$\sqrt{61}$ʱ��y=S��ABQ-S��APQ-S��ABP=$\frac{1}{2}$•6•��8-2x��-$\frac{1}{2}$•��8-2x��•$\frac{3}{5}$x-$\frac{1}{2}$•8•$\frac{4}{5}$x=$\frac{3}{5}$x2-$\frac{58}{5}$x+24��
��18-2$\sqrt{61}$��x��4ʱ��y=S��APQ+S��ABP-S��ABQ=$\frac{1}{2}$•��8-2x��•$\frac{3}{5}$x+$\frac{1}{2}$•8•$\frac{4}{5}$x-$\frac{1}{2}$•6•��8-2x��=-$\frac{3}{5}$x2+$\frac{58}{5}$x-24��
���� ���⿼����ε����ʡ�ƽ���߷��߶γɱ������������ɶ�������ֱ�������ε�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮


 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�AB=AC��O�ǡ�ABC��һ�㣬��OB=OC�����ж�AO��BC��λ�ù�ϵ��
��ͼ���ڡ�ABC�У�AB=AC��O�ǡ�ABC��һ�㣬��OB=OC�����ж�AO��BC��λ�ù�ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���� | 10��1�� | 10��2�� | 10��3�� | 10��4�� | 10��5�� | 10��6�� | 10��7�� |
| ���������ˣ� | 1.2 | 2 | 2.5 | 2 | 1.2 | 2 | 0.6 |
| A�� | 1.2��2�� | B�� | 2��2.5�� | C�� | 2��2�� | D�� | 1.2��2.5�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com