
【题目】已知:如图,一块Rt△ABC的绿地,量得两直角边AC=8cm,BC=6cm.现在要将这块绿地扩充成等腰△ABD,且扩充部分(△ADC)是以8cm为直角边长的直角三角形,求扩充等腰△ABD的周长.
(1)在图1中,当AB=AD=10cm时,△ABD的周长为 .
(2)在图2中,当BA=BD=10cm时,△ABD的周长为 .
(3)在图3中,当DA=DB时,求△ABD的周长.

【答案】(1)32m;(2)(20+4![]() )m;(3)
)m;(3)![]()
【解析】
(1)利用勾股定理得出DC的长,进而求出△ABD的周长;
(2)利用勾股定理得出AD的长,进而求出△ABD的周长;
(3)首先利用勾股定理得出DC、AB的长,进而求出△ABD的周长.
:(1)如图1,∵AB=AD=10m,AC⊥BD,AC=8m,
∴![]()
则△ABD的周长为:10+10+6+6=32(m).
故答案为:32m;
(2)如图2,当BA=BD=10m时,
则DC=BD-BC=10-6=4(m),
故![]()
则△ABD的周长为:AD+AB+BD=10+4![]() +10=(20+4
+10=(20+4![]() )m;
)m;
故答案为:(20+4![]() )m;
)m;
(3)如图3,∵DA=DB,
∴设DC=xm,则AD=(6+x)m,
∴DC2+AC2=AD2,
即x2+82=(6+x)2,
解得;x=![]()
∵AC=8m,BC=6m,
∴AB=10m,
故△ABD的周长为:AD+BD+AB=2![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
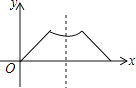
【题目】已知点P为某个封闭图形边界上的一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )
A. 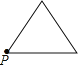 B.
B. 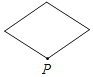 C.
C. 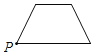 D.
D. 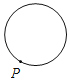
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
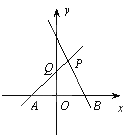
【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线![]() .下列结论中,正确的是( )
.下列结论中,正确的是( )

A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件42元的价格购进一种服装,由试销知,每天的销量t与每件的销售价x(元)之间的函数关系为t=204-3x。
(1)试写出每天销售这种服装的毛利润y(元)与每件销售价x(元)之间的函数表达式(毛利润=销售价-进货价); 并求出自变量的取值范围。
(2)每件销售价为多少元,才能使每天的毛利润最大?最大毛利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为![]() 、宽为
、宽为![]() 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)
的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)

(1)观察图2请你写出![]() 、
、![]() 、
、![]() 之间的等量关系是______;
之间的等量关系是______;
(2)根据(1)中的结论,若![]() ,
,![]() ,则
,则![]() ______;
______;
(3)拓展应用:若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
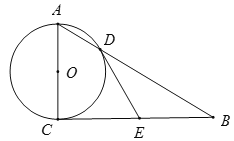
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系:_________;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC=_______时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com